Простое гармоническое движение
Простым гармоническим движением назвается движение, при котором сила сопротивления движения пропорциональна перемещению.
Простое гармоническое движение выполняется бесконечно долго, поскольку не учитываются силы трения или какие-либо другие силы. Конечно же, это идеализированный вариант, который не встречается в повседневной жизни.
В качестве примера простого гармонического движения рассмотрим движение груза, прикрепленного к пружине.
В начальный момент времени, когда на груз не действуют никакие силы, груз и пружина находятся в состоянии покоя (равновесия).
Если груз оттянуть вниз, растянув тем самым пружину, а затем отпустить, то под возникшей в пружине упругой силе сопротивления, пружина начнет сжиматься, а груз - двигаться вверх, стремясь вернуться в положение равновесия.
Когда груз достигнет точки положения равновесия, он будет обладать некоей скоростью (импульсом), и продолжит движение дальше, сжимая пружину до некоторого значения.
После того, как силы уравновесятся, груз будет находиться в крайней верхней точке, после чего упругая сила пружины заставит пружину распрямляться, и груз пойдет вниз, пройдет точку положения равновесия, и достигнув крайней нижней точки, снова пойдет вверх.
В нашем эксперименте мы не учитываем силу трения, тяжести, сопротивления воздуха, воздействие которых постепенно приведет к тому, что амплитуда движения груза будет становиться все меньше и меньше, пока груз и пружина не замрут в точке равновесия.
Если же на систему груз+пружина не будут воздействовать никакие посторонние силы, то колебание груза будет бесконечным.
Периодические движения подобного рода называются периодическими колебаниями, а расстояние между крайними положениями тела - амплитудой колебания.
Если рассмотреть движение пружины с грузом во времени, то можно заметить, что груз движется по синусоидальной кривой.
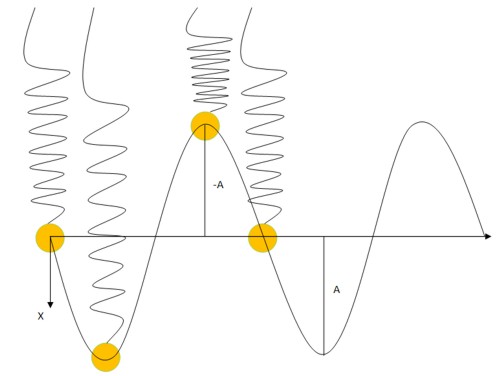
Груз будет совершать периодические движение вверх-вниз, относительно исходного положения равновесия, с амплитудой А. Вблизи точки равновесия груз будет обладать максимальной скоростью, а в точках амплитуды скорость груза будет нулевой.
Аналогичную синусоидальную кривую будет описывать груз, движущийся по окружности, расположенной перпендикулярно плоскости экрана.
Если расположить окружность параллельно плоскости экрана, то положение груза можно определить по формуле: x=A(cosΘ) (см. рисунок ниже):
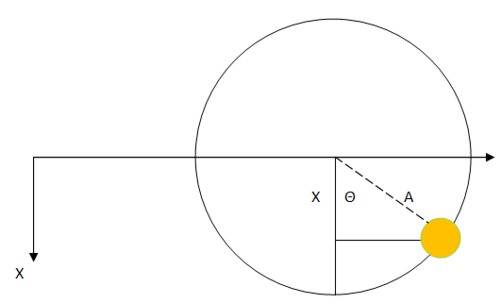
- x - текущее смещение груза по оси Х от положения равновесия;
- Θ - угол поворота груза при вращении по окружности;
- А - амплитуда периодического движения.
Если угловая скорость движения груза по окружности постоянна, то:
Θ = ωt x = A·cos(ωt)
Циклом вращательного движения называется путь, равный длине окружности, пройденный грузом.
Периодом вращательного движения называется время прохождения цикла.
На рисунках выше, полный цикл равняется движению груза от точки равновесия (исходное положение) до нижней точки (А), затем, до верхней точки (-А), и снова к точке равновесия (полная синусоида).
Таким образом, можно утверждать, что за один полный цикл груз проходит угол, равный 2π за период Т, при этом угловая скорость груза равна:
ω = 2π/T T = (2π)/ω
Одной из важнейших характеристик периодического движения является его частота - кол-во циклов за единицу времени: f=1/T
Как видно из формулы, частота является величиной, обратно пропорциональной периоду. Например, если за 1 с объект совершает 10 полных циклов (оборотов), то говорят, что объект вращается с частотой 10 с-1 или с периодом 0,1 с.
Исходя из вышесказанного, находим связь между частотой и угловой скоростью:
T = (2π)/ω ω = 2π/T = 2πf
Угловую скорость ω при описании периодичеких движений принято называть циклической частотой.
Скорость в простом гармоническом движении
При движении тела по окружности, его координата перемещения по оси Х определяется формулой:
x = A·cos(ωt)
- x - текущее смещение тела от положения равновесия по оси Х;
- ω - угловая скорость тела при движении по окружности;
- A - амплитуда периодического движения тела.
В некоторой точке с координатой х тело будет обладать определенной скоростью, которая будет зависеть от времени. Попробуем вывести формулу для определения скорости тела в любой момент времени его движения по окружности.
Угловая и тангенциальная скорости связаны соотношением (см. Параметры вращательного движения):
v = rω
В нашем случае r=A:
v = Аω
Для определения скорости периодических колебаний тела по оси Х находим проекцию тангенциальной скорости на ось Х:
vx = v·sin(β) = -v·sin(Θ)
Подставим в формулу значения Θ=ωt и v=A·ω:
vx = -Aω·sin(ωt)
В простом гармоническом движении амплитуда скорости Аv=Aω связана с амплитудой перемещения Ax=A формулой: Av = -Axω.
Ускорение в простом гармоническом движении
Со скоростью вращающегося объекта мы разобрались, теперь попробуем вывести формулу для определения центростремительного ускорения (действовать будем аналогично).
Вспомним формулу, связывающую угловую скорость и центростремительное ускорение (см. Параметры вращательного движения):
a = rω2
Поскольку, для нашего случая r=A, получаем:
a = Аω2
Вычисляем проекцию центростремительного ускорения на ось Х:
аx = a·cos(γ) = -a·cos(Θ)
Подставим в формулу значения Θ=ωt и a=A·ω2:
ax = -Aω2·cos(ωt)
В простом гармоническом движении амплитуда ускорения Аа=Aω2 связана с амплитудой перемещения Ax=A формулой: Aа = -Axω2.
Частота колебаний груза на пружине
Из закона Гука и второго закона Ньютона вытекает следующее равенство:
F = -kx F = ma ma = -kx
Перемещение и ускорение в простом гармоническом движении описываются формулами:
x = A·cos(ωt) a = -Aω2cos(ωt)
Подставляем выражения в предыдущую формулу:
m(-Aω2cos(ωt)) = -k(A·cos(ωt)) m·ω2 = k ω = √(k/m)
Вспоминаем о цикле и периоде: ω=2πf и ω=2π/T:
f = (1/2π)·√(k/m) T = 2π·√(m/k)
Применим полученные теоретические знания на практике.
Исходные данные:
- коэффициент упругости пружины k=1 Н/м
- к пружине прикреплен груз массой m=1 кг
- чему равен период и частота колебаний груза на пружине?
T = 2π·√(m/k) = 6,28·√(1/1) = 6,28 с f = (1/2π)·√(k/m) = 0,16 Гц
Зная формулы перемещения, скорости и ускорения для простого гармонического движения, можно вычислить координаты, скорость и ускорение груза на пружине в любой момент времени.
x = A·cos(ωt) vx = -Aω·sin(ωt) a = -Aω2cos(ωt)
Допустим, что амплитуда А=1 м.
Определяем циклическую частоту:
ω = √(k/m) = 1 с-1
Теперь подставляем числовые значения в формулы:
x = cos(t) vx = -sin(t) a = -cos(t)
