Физические основы классической механики
Механика - раздел физики, который изучает одну из простейших и наиболее общих форм движения в природе, называемую механическим движением.
Механическое движение заключается в изменении с течением времени положения тел или их частей друг относительно друга. Так механическое движение совершают планеты, обращающиеся по замкнутым орбитам вокруг Солнца; различные тела, перемещающиеся по поверхности Земли; электроны, движущиеся под действием электромагнитного поля и т.д. Механическое движение присутствует в других более сложных формах материи как составная, но не исчерпывающая часть.
В зависимости от характера изучаемых объектов механика подразделяется на механику материальной точки, механику твердого тела и механику сплошной среды.
Принципы механики впервые были сформулированы И. Ньютоном (1687 год) на основе экспериментального изучения движения макротел с малыми по сравнению со скоростью света в вакууме (3·108 м/с) скоростями.
Макротелами называют обычные тела, окружающие нас, то есть тела, состоящие из громадного количества молекул и атомов.
Механику, изучающую движение макротел со скоростями намного меньшими скорости света в вакууме, называют классической.
В основе классической механики лежат следующие представления Ньютона о свойствах пространства и времени.
Любой физический процесс протекает в пространстве и времени. Это видно хотя бы из того, что во всех областях физических явлений каждый закон явно или неявно содержит пространственно-временные величины - расстояния и промежутки времени.
Пространство, имеющее три измерения, подчиняется эвклидовой геометрии, то есть является плоским.
Расстояния измеряются масштабами, основным свойством которых является то, что два однажды совпавших по длине масштаба всегда остаются равными друг другу, то есть при каждом последующем наложении совпадают.
Промежутки времени измеряются часами, причем роль последних может выполнять любая система, совершающая повторяющийся процесс.
Основной чертой представлений классической механики о размерах тел и промежутках времени является их абсолютность: масштаб всегда имеет одну и туже длину, независимо от того, как он движется относительно наблюдателя; двое часов, имеющих одинаковый ход и приведенные однажды в соответствие друг другу, показывают одно и тоже время независимо от того, как они движутся.
Пространство и время обладают замечательными свойствами симметрии, налагающими ограничения на протекание в них тех или иных процессов. Эти свойства установлены на опыте и кажутся на первый взгляд столь очевидными, что, вроде бы, и нет надобности выделять их и заниматься ими. А между тем, не будь пространственной и временной симметрии, никакая физическая наука не могла бы ни возникнуть, ни развиваться.
Оказывается, пространство однородно и изотропно, а время - однородно.
Однородность пространства состоит в том, что одинаковые физические явления в одних и тех же условиях совершаются одинаково в различных частях пространства. Все точки пространства, таким образом, совершенно неразличимы, равноправны и любая из них может быть принята за начало системы координат. Однородность пространства проявляется в законе сохранения импульса.
Пространство обладает еще и изотропностью: одинаковостью свойств во всех направлениях. Изотропность пространства проявляется в законе сохранения момента импульса.
Однородность времени заключается в том, что все моменты времени также равноправны, эквивалентны, то есть протекание одинаковых явлений в одних и тех же условия одинаково, безотносительно ко времени их осуществления и наблюдения.
Однородность времени проявляется в законе сохранения энергии.
Не будь этих свойств однородности, установленный в Минске физический закон был бы несправедлив в Москве, а открытый сегодня в том же месте мог бы быть несправедлив завтра.
В классической механике признается справедливость закона инерции Галилея-Ньютона, согласно которому тело, не подверженное действию со стороны других тел, движется прямолинейно и равномерно. Этот закон утверждает существование инерциальных систем отсчета, в которых выполняются законы Ньютона (а также принцип относительности Галилея). Принцип относительности Галилея утверждает, что все инерциальные системы отсчета эквивалентны друг другу в механическом отношении, все законы механики одинаковы в этих системах отсчета, или, другими словами, инвариантны относительно преобразований Галилея, выражающих пространственно-временную связь любого события в разных инерциальных системах отсчета. Преобразования Галилея показывают, что координаты любого события относительны, то есть имеют разные значения в разных системах отсчета; моменты же времени, когда событие произошло, одинаковы в разных системах. Последнее означает, что время течет одинаковым образом в разных системах отсчета. Это обстоятельство казалось столь очевидным, что даже не оговаривалось как специальный постулат.
В классической механике соблюдается принцип дальнодействия: взаимодействия тел, распространяются мгновенно, то есть с бесконечно большой скоростью.
В зависимости от того, с какими скоростями происходят перемещения тел и каковы размеры самих тел, механика подразделяется на классическую, релятивистскую, квантовую.
Как уже указывалось, законы классической механики применимы лишь к движению макротел, масса которых гораздо больше массы атома, с малыми скоростями по сравнению со скоростью света в вакууме.
Релятивистская механика рассматривает движение макротел со скоростями, близкими к скорости света в вакууме.
Квантовая механика - механика микрочастиц, движущихся со скоростями намного меньшими скорости света в вакууме.
Релятивистская квантовая механика - механика микрочастиц, движущихся со скоростями, приближающимися к скорости света в вакууме.
Чтобы определить принадлежит ли частица к макроскопическим, применимы ли к ней классические формулы, нужно воспользоваться принципом неопределенности Гейзенберга. Согласно квантовой механики реальные частицы могут быть охарактеризованы с помощью координаты и импульса лишь с некоторой точностью. Предел этой точности определяется так
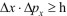
где
ΔX - неопределенность координаты;
ΔPx - неопределенность проекции на ось импульса;
h - постоянная Планка, равная 1,05·10-34 Дж·с;
"≥" - больше величины, порядка …
Заменив импульс произведением массы на скорость, можно написать
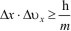
Из формулы видно, что чем меньше масса частицы, тем менее определенными делаются ее координаты и скорость. Для макроскопических тел практическая применимость классического способа описания движения не вызывает сомнений. Допустим, например, что речь идет о движении шарика с массой в 1 г. Обычно положение шарика практически может быть определено с точностью до десятой или сотой доли миллиметра. Во всяком случае, вряд ли имеет смысл говорить об ошибке в определении положения шарика, меньшей размеров атома. Положим поэтому ΔX=10-10м. Тогда из соотношения неопределенностей найдем
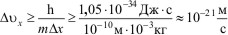
Одновременная малость величин ΔX и ΔVx и является доказательством практической применимости классического способа описания движения макротел.
Рассмотрим движение электрона в атоме водорода. Масса электрона 9,1·10-31 кг. Ошибка в положении электрона ΔX во всяком случае не должна превышать размеры атома, то есть ΔX<10-10м. Но тогда из соотношения неопределенностей получаем
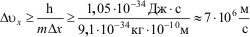
Эта величина даже больше скорости электрона в атоме, которая по порядку величины равна 106м/с . При таком положении классическая картина движения теряет всякий смысл.
Механику подразделяют на кинематику, статику и динамику. Кинематика описывает движение тел, не интересуясь причинами, обусловившими это движение; статика рассматривает условия равновесия тел; динамика изучает движение тел в связи с теми причинами (взаимодействиями между телами), которые обусловливают тот или иной характер движения.
Реальные движения тел настолько сложны, что, изучая их, необходимо отвлечься от несущественных для рассматриваемого движения деталей (в противном случае задача так усложнилась бы, что решить ее практически было бы невозможно). С этой целью используют понятия (абстракции, идеализации), применимость которых зависит от конкретного характера интересующей нас задачи, а также от степени точности, с которой мы хотим получить результат. Среди этих понятий большую роль играют понятия материальной точки, системы материальных точек, абсолютно твердого тела.
Материальная точка - это физическое понятие, с помощью которого описывается поступательное движение тела, если только его линейные размеры малы в сравнении с линейными размерами других тел в рамках заданной точности определения координаты тела, причем, ей приписывается масса тела.
В природе материальных точек не существует. Одно и то же тело в зависимости от условий можно рассматривать или как материальную точку, или как тело конечных размеров. Так, Землю, движущуюся вокруг Солнца, можно считать материальной точкой. Но при изучении вращения Земли вокруг своей оси ее уже нельзя считать материальной точкой, так как на характер этого движения существенно влияют форма и размеры Земли, и путь, проходимый какой-либо точкой земной поверхности за время, равное периоду ее обращения вокруг своей оси, сравним с линейными размерами земного шара. Самолет можно рассматривать как материальную точку, если изучать движение его центра масс. Но если необходимо учитывать влияние среды или определить усилия в отдельных частях самолета, то мы должны рассматривать самолет как абсолютно твердое тело.
Абсолютно твердым телом называют тело, деформациями которого в условиях данной задачи можно пренебречь.
Система материальных точек - это совокупность рассматриваемых тел, представляющих собой материальные точки.
Изучение движения произвольной системы тел сводится к изучению системы взаимодействующих материальных точек. Естественно, поэтому начать изучение классической механики с механики одной материальной точки, а затем перейти к изучению системы материальных точек.
