Простые и составные числа
Простыми натуральными числами называются числа, которые делятся без остатка только на единицу и самое себя.
13:1 = 13; 13:13 = 1
Составными натуральными числами называются числа, которые имеют более двух натуральных делителей, т. е., кроме единицы и самое себя еще имеют другие делители, на которые делятся без остатка.
14:1 = 14 14:2 = 7 14:7 = 2 14:14 = 1
1 (единица) - не является ни простым, ни составным числом, т.к. имеет всего один натуральный делитель - 1.
2 (двойка) - является единственным четным простым числом.
Любое составное число можно разложить на простые множители:
100 = 2·2·5·5
Таким образом, можно сказать, что все множество натуральных чисел состоит из суммы двух множеств - множества простых чисел и множества составных чисел.
Таблица простых чисел от 1 до 1000
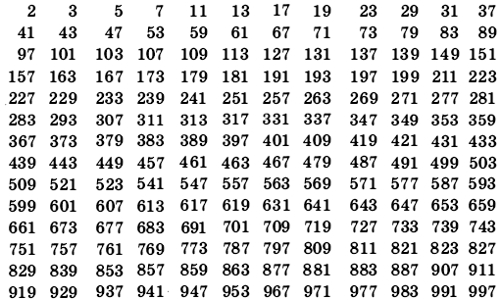
Разложение составных чисел на простые множители
Разложение небольших чисел на простые множители, как правило, не составляет труда. А вот с числами крупными все обстоит уже не так очевидно.
Для того, чтобы разложить большое число на простые множители, пользуются таблицей простых чисел (см. выше) и признаками делимости.
Порядок разложения натурального числа на простые множители следующий:
- по признакам делимости находится первый из простых чисел делитель: 2, 3, 5, 7, 11;
- исходное число делится на первый найденный "простой" делитель, дальше продолжают работать с получившимся остатком (см. п.1).
Примеры разложения натуральных чисел на простые делители
В качестве примера разложим на простые делители число 777:
- первым делом смотрим в таблицу простых чисел (см. выше) и видим, что число 777 не является простым;
- начинаем поиск наименьшего простого делителя;
- первым простым делителем числа 777 будет число 3 - это сразу понятно, т.к. 2 не подходит, т.к. 777 число нечетное, а 3 подходит, и тут даже не надо складывать цифры числа, поскольку в числе 777 присутствует 3 одинаковых цифры: 777:3=259;
- снова проверяем по таблице, является ли число 259 простым числом - нет, не является, значит, продолжаем его разложение на простые множители;
- первым простым делителем числа 259 будет число 7: 259:7=37;
- смотрим снова в таблицу простых чисел, и видим, что число 37 является простым числом, значит разложение закончено;
- Результат: 777=2·7·37.
Возьмем число побольше, например, 27359850:
- сразу раскроем небольшой "секрет" - если число кратно 10, то сразу имеются два простых множителя, произведение которых дает 10 - это 2 и 5: 2·5=10;
- поэтому, "со старта" уже имеем два простых множителя 2 и 5, а исходное число уменьшается на 10;
- работаем дальше с числом 2735985 - это нечетное число, поэтому, 2 отбрасывается;
- сумма цифр в числе 2735985 кратна 3, значит, следующим простым множителем будет 3: 2735985:3=911995;
- число 91195 не кратно ни 2, ни 3, но кратно 5: 91195:5=18239;
- следующим наименьшим простым делителем будет число 13: 18239:13=1403;
- следующим наименьшим простым делителем будет число 23: 1403:23=61;
- 61 является простым числом - разложение закончено;
- Результат: 27359850=2·3·5·5·13·23·61.
