Как решать тригонометрические неравенства
Тригонометрическим называется неравенство, одна часть которого представлена тригонометрической функцией, а вторая - числовым выражением:
Примеры тригонометрических неравенств:
sin(x)<0 cos(x)≥1 tg(x)>1/3
Решать тригонометрические неравенства удобно при помощи единичной окржности, по аналогии с решением квадратных неравенств при помощи эскиза параболы.
Алгоритм решения тригонометрических неравенств при помощи единичной окружности:
- определить дугу единичной окружности, для всех точек которой будет выполняться исходное неравенство;
- найти центральные углы, одной стороной которых является луч, начинающийся в точке начала координат и совпадающей с положительным направлением оси абсцисс, а другая сторона пересекает данную дугу;
- к найденному решению следует прибавить период рассматриваемой тригонометрической функции к обеим частям полученного неравенства.
Пример 1: Решить неравенство sin(x)>1/2.
1. Находим дугу единичной окружности, точки которой будут удовлетворять исходному неравенству. Сделать это очень просто - на оси ординат отмечаем точку ½ и из нее проводим горизонтальную линию до пересечения с единичной окружностью. Все точки окружности, которые будут лежать выше проведенной горизонтали, составят искомую дугу, т. к. ординаты этих точек больше ½.
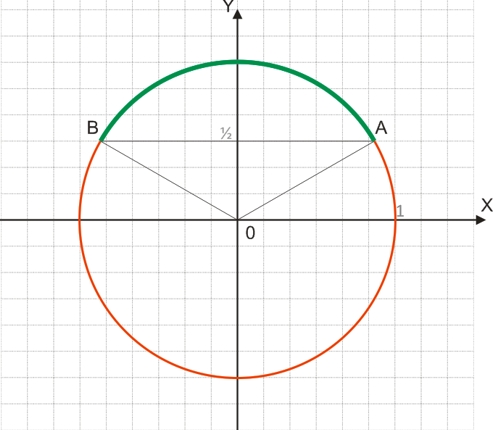
2. Ордината угла AOX может быть вычислена по формуле y=arcsin(XOA). Точно такую же ординату будет иметь угол XOB: y=arcsin(XOB)=arcsin(XOA). Это логично вытекает из того обстоятельства, что в пределах одной и той же единичной окружности синусы углов α и π-α равны (см. Свойства тригонометрических функций).
3. В нашем неравенстве фигурируют углы, ординаты которых равны ½. В правой полуокружности такая ордината будет у угла arcsin(½); в левой: π-arcsin(½). Поскольку нас интересуют точки окружности, ординаты которых больше ½, то решение нашего неравенства будет следующее:
arcsin(½)+2kπ < x < π-arcsin(½)+2kπ
Пример 2: Решить неравенство cos(x)>1/2.
1. Находим дугу единичной окружности, точки которой будут удовлетворять исходному неравенству. Сделать это очень просто - на оси абсцисс отмечаем точку ½ и из нее проводим вертикальную линию до пересечения с единичной окружностью. Все точки окружности, которые будут лежать правее проведенной вертикали, составят искомую дугу, т. к. абсциссы этих точек больше ½.
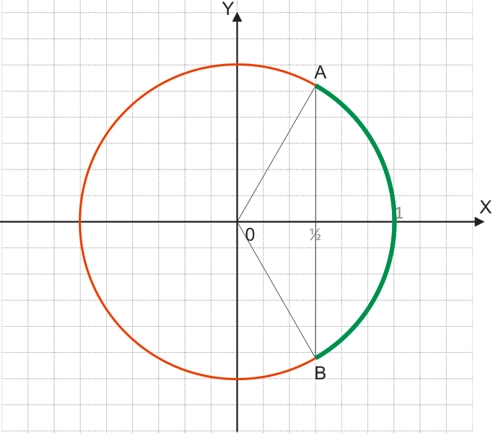
2. Поскольку, в пределах одной и той же единичной окружности cos(α)=cos(-α), поэтому абсциссу ½ будут иметь два угла: XOA и XOB: arccos(½) и arccos(-½).
3. Таким образом, решением исходного неравенства в пределах единичной окружности будут все углы, полученные вращением против часовой стрелки радиуса ОВ до совмещения с радиусом ОА, исключая при этом углы XOA, XOB:
arccos(-½)+2kπ < x < arccos(½)+2kπ
