Что такое радиан
Радиан, как и градус, является угловой мерой, т. е., величиной, при помощи которой измеряются плоские углы.
1 радиан - это центральный угол окружности радиуса r, который опирается на дугу, длина которой равна радиусу r.
Возьмем окружность, радиусом r:
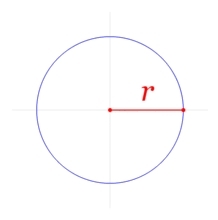
Отложим на окружности дугу, длиной, равной радиусу r, при этом концы дуги соединим с центром окружности:
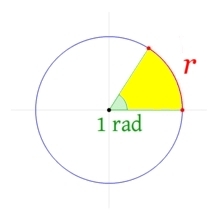
Это и есть угол в 1 радиан.
1 радиан примерно равен 57°.
Радиан является единицей измерения плоских углов в системах СИ и СГС.
Радиан - безразмерная единица, поскольку является отношением длины дуги окружности (измеряется в метрах), заключенной между сторонами угла, к радиусу этой окружности (также измеряется в метрах).
Длина окружности (С) связана с ее радиусом (r) следующим соотношением:
C=2πr
Поэтому, развернутый угол будет опираться на дугу, длина которой будет равна πr, такой угол будет равен π радиан.
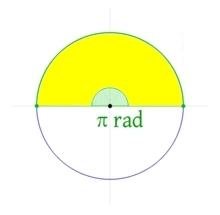
Слово "радиан" не принято писать.
Поскольку развернутый угол с одной стороны равен 180°, а с другой - это π радиан, то:
1° = 180/π
Поскольку, на 1° приходится π/180 радиан, то угол в α° будет содержать в α раз больше радиан, чем 1°.
С другой стороны, на 1 радиан приходится (180/π)°, поэтому, на угол β радиан будет приходиться в β раз больше градусов, чем на 1 радиан.
α° = (β·180°)/π β = (α°·π)/180°
При помощи этих формул легко переводить градусы в радианы и обратно. Например, угол в 60° будет равен:
β = (60°·π)/180° = π/3 радиан
Угол в 1,5 радиана будет равен:
α° = (1,5·180°)/3,14 ≈ 90°
