Чему равна площадь треугольника
Площадь треугольника можно найти одним из трех способов, изложенных ниже:
- Площадь треугольника равна половине произведения одной из его сторон на высоту, опущенную на эту сторону;
- Площадь треугольника равна половине произведения двух любых его сторон на синус угла, расположенного между этими сторонами;
- Площадь треугольника можно вычислить по формуле Герона, которая позволяет найти площадь, зная длину всех сторон треугольника.
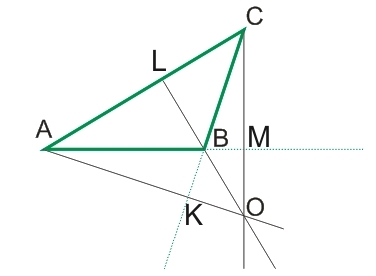
- SABC=½·AB·CM
- SABC=½·BC·AK
- SABC=½·CA·BL
- SABC=½·AB·AC·sin(∠CAB)
- SABC=½·BC·BA·sin(∠ABC)
- SABC=½·CA·CB·sin(∠BCA)
Формула Герона:
√p(p-a)(p-b)(p-c) a,b,c - стороны треугольника p=(a+b+c)/2
Например, если стороны прямоугольника равны 3, 4, 5 см, то его площадь будет равна:
p=(3+4+5)/2=6 √6(6-3)(6-4)(6-5)=√36=6см2
