Электрическое поле
Для того, чтобы найти силу, которая действует между двумя электрическими зарядами, надо знать значение каждого из них и расстояние между зарядами. Если таких зарядов два, задача легко решается при помощи закона Кулона. А как быть, когда электрических зарядов много? Для таких случаев физики ввели понятия электрического поля.
При помощи электрического поля можно описать, как множество зарядов будет воздействовать на некий пробный заряд, который может быть помещен в любую точку электрического поля. Для этого достаточно умножить величину пробного заряда на величину напряженности поля в той точке, где находится пробный заряд.
E = F/q (Н·Кл-1)
- E - напряженность электрического поля;
- F - сила, которая действует на пробный заряд со стороны множества зарядов;
- q - величина пробного заряда.
Напряженность электрического поля является векторной величиной, имеет свой модуль и направление. Если заряд в точке положительный - направление силы совпадает с направлением напряженности поля в этой точке; если заряд отрицательный - сила направлена в противоположную сторону.
Напряженность электрического поля в любой точке является результирующим вектором, и вычисляется путем сложения составляющих векторов электрических полей.
Электрическое поле точечного заряда
Под точечным зарядом понимается заряд очень малого физического объекта.
Точечный заряд Q создает некое электрическое поле. При этом, с помощью пробного заряда q можно измерить в разных точках силу, которую вызывает заряд Q:
F = kqQ/r2 E = F/q = kQ/r2
Напряженность электрического поля точечного заряда является векторной величиной, она направлена по прямой, соединяющей центры двух зарядов, при этом линии поля выходят из положительных зарядов и сходятся у отрицательных зарядов. Данная модель была впервые предложена в 19 веке Майклом Фарадеем.
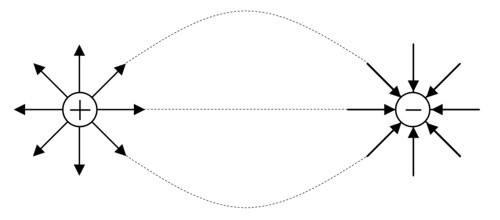
Надо понимать, что линии электрического поля не могут начинаться и заканчиваться в некой точке пространства, где нет электрического заряда.
Для того, чтобы определить величину электрического поля от нескольких зарядов в конкретной точке поля, необходимо сложить векторы напряженности полей в этой точке.
Электрическое поле плоского конденсатора
Следует признать, что задача вычисления электрического поля от множественных точечных зарядов, достаточно сложна. Физики, как народ достаточно "ленивый", решили для упрощения задачи использовать модели простых электрических полей, например, плоский конденсатор.
В электрическом конденсаторе положительные и отрицательные заряды хранятся отдельно - каждый на своей пластине, при этом они притягиваются, но не соединяются, т.к. пластины конденсатора разделены диэлектриком.
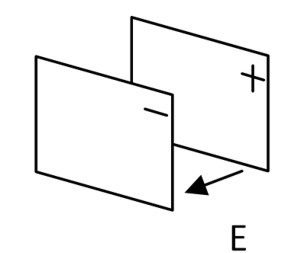
Допустим, дальняя пластина конденсатора на верхнем рисунке заряжена положительно (на пластине равномерно распределены точечные заряды +q), а нижняя - отрицательно (на пластине равномерно распределены точечные заряды -q). При этом все компоненты напряженностей электрических полей, которые создаются точечными зарядами, взаимно компенсируют друг друга, за исключением компонент, направленных перпендикулярно пластинам конденсатора. Таким образом, между двумя пластинами плоского конденсатора, расположенными параллельно друг другу, создается постоянное электрическое поле, напряженность которого можно вычислить по формуле:
E = q/(ε0A)
- ε0≈8,85·10-12Кл2Н-1м-2 - электрическая постоянная.
- q - общий заряд для каждой из пластин.
- А - площадь каждой пластины.
Отношение q/A называется плотностью заряда σ (характеризует заряд, который приходится на единицу площади). В таком случае, напряженность поля будет равна:
E = σ/ε0
Такая модель плоского конденсатора значительно упрощает задачу поиска напряженности электрического поля, поскольку она постоянна и имеет постоянное направление (с положительной пластины на отрицательную), поэтому, напряженность электрического поля будет одинаковой в любом месте между пластинами конденсатора.
