Электрический потенциал
Из курса Механики известно, что потенциальная энергия тела связана с работой силы, например, подъем груза в гравитационном поле увеличивает его потенциальную энергию.
Поскольку, в электрическом поле на заряды также действуют силы, понятие потенциальной энергии будет справедливо и для электрических полей, при этом изменение потенциальной энергии электрического поля является движущей силой электрического тока, и называется напряжением.
Предположим, что в электрическом поле плоского конденсатора положительно заряженный одиночный заряд движется по направлению к положительной пластине, как показано на рисунке ниже.
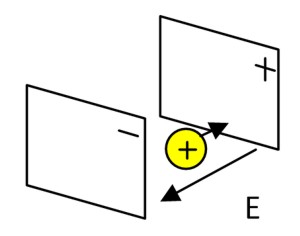
На одиночный заряд со стороны положительной пластины будет действовать отталкивающая сила, а со стороны отрицательной - притягивающая. Определим изменение потенциальной энергии одиночного положительного заряда при его перемещении между пластинами конденсатора, против сил, действующих в противоположном направлении.
Работа, выполняемая одиночным зарядом, будет равна:
A = Fs
- F - сила, действующая на заряд;
- s - перемещение заряда.
В свою очередь:
F = qE тогда A = qEs
- q - величина заряда;
- E - напряженность электрического поля.
Данная величина работы будет равна увеличению потенциальной энергии заряда ΔW:
ΔW = qEs
Электрическое поле в физике характеризуется его напряженностью - силой, действующей со стороны поля на точечный заряд в 1 Кл.
Изменение потенциальной энергии электрического поля между двумя точками описывается электрическим напряжением или разностью потенциалов.
Разность потенциалов определяется, как отношение работы электрического поля при переносе электрического заряда из одной точки в другую к его величине.
U = W/q
Поскольку, A = qEs, т.е., работа равна изменению потенциальной энергии заряда при перемещении на расстояние s от отрицательной пластины, поэтому, электрический потенциал в месте нахождения электрического заряда будет равен:
U = W/q = Es
Электрический потенциал точечного заряда
Определить потенциал точечного заряда Q будет сложнее, поскольку его электрическое поле не такое постоянное, как в конденсаторе, и зависит от расстояния до течечного объекта:
F = (kQq)/r2
- F - сила, действующая на пробный заряд;
- Q - заряд точечного объекта;
- q - заряд пробного объекта, помещенного в электрическое поле объекта Q;
- r - расстояние между точечным зарядом Q и пробным зарядом q;
- k=8,99·109 Н·м2/Кл2
Напряженность электрического поля в любой точке вокруг точечного заряда определяется по формуле:
F = (kQ)/r2
Изменение электрического потенциала пробного заряда равно выполненной работе, деленной на величину пробного заряда:
U = A/q = kQ/r
- U - разность потенциалов;
- A - работа.
Чем больше расстояние r, тем ниже потенциал (при r=∞ U=0).
Электрический потенциал, как и электрическое поле можно представить графически в виде эквипотенциальных поверхностей (поверхности с одинаковым потенциалом). Поскольку, величина потенциала точечного заряда зависит от расстояния, то эквипотенциальными поверхностями точечного заряда являются сферы, в центре которых находится точечный заряд. Соответственно эквипотенциальными поверхностями плоского конденсатора будут плоскости, расположенные параллельно пластинам конденсатора.
Емкость конденсатора
Выше уже было сказано, что на пластинах конденсатора хранятся противоположные по знаку электрические заряды, которые притягиваются друг к другу, но не могут соединиться. А сколько зарядов может находиться на пластинах конкретного конденсатора, говоря другими словами, каков заряд конденсатора?
Заряд конденсатора определяется его емкостью, и связан с напряжением между пластинами следующей формулой:
q = CU
- q - заряд пластин конденсатора;
- C - емкость конденсатора;
- U - напряжение между пластинами конденсатора.
Для плоского конденсатора напряженность его электрического поля определяется по формуле:
E = q/(ε0A)
- A - площадь пластины конденсатора;
- ε0 - электрическая постоянная
Поскольку, для плоского конденсатора U=Es, то U=(qs)/(ε0A).
Подставив в формулу значение заряда q=CU, получаем формулу емкости конденсатора (измеряется в Фарадах):
C = q/U = (ε0A)/s Кл/В или Ф
В реальных конденсаторах, которые применяются в электрических схемах приборов и устройств, пластины конденсатора разделены не воздухом, а диэлектриком (веществом, которое плохо проводит электричество). Применение диэлектрика дает возможность инженерам конструировать малогабаритные конденсаторы достаточно большой емкости, чего простой воздух делать не позволяет.
Емкость конденсатора увеличивается пропорционально диэлектрической проницаемости диэлектрика ε:
C = q/U = (εε0A)/s
Проведя несложные расчеты, можно вывести формулу для определения энергии конденсатора:
W = 1/2CU2 Дж
