Что такое производная функции
Забегая немного вперёд, сразу скажем о смысле производной функции в общем случае.
| Производная показывает скорость изменения функции при изменении её аргумента |
На страницах График равномерного движения и График равноускоренного движения при определении мгновенной скорости рассматривались отношения следующего вида:
(s0-s1)/(t0-t1)
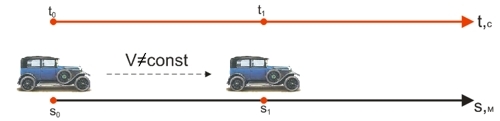
Отличительной особенностью этого отношения являлся тот факт, что мы пытались определить перемещение тела за как можно малый промежуток времени, т.е. при очень близких значениях t0 и t1.
Проблема заключается в том, что математика является точной наукой, и не приемлет выражения типа "как можно малый промежуток", ибо оно является неопределённым и может трактоваться как угодно. Для подобных случаев математики придумали понятия предела - нечто такое, к чему мы стремимся, но никогда не достигнем (например, многие рядовые обыватели стремятся стать миллионерами, и чем больше денег зарабатывают, тем ближе становятся к цели, которую так никогда и не достигнут).
Для нахождения мгновенной скорости необходимо найти предел, к которому стремится отношение:
(s0-s1)/(t0-t1)
при t1 стремящемся к t0.
В математике для удобства записей принято разность обозначать значком "дельта":
s0-s1 = Δs t0-t1 = Δt
С учётом новых обозначений формулу для нахождения средней скорости можно записать в следующем виде:
vср = Δs/Δt
Обратите внимание, что значок Δ не является множителем, и проводить стандартные арифметические действия с ним нельзя.
Запись Δs (дельта эс) можно читать, как "приращение расстояния"; запись Δt (дельта тэ) - "приращение времени".
Собственно в значке Δ и заключена та самая неопределенность величины разности между двумя значениями s или t.
Ещё один очень важный момент, который следует изначально правильно понимать - в формуле Δs/Δt числитель и знаменатель зависимы - изначально можно выбрать любой промежуток времени Δt, но, после того, как он выбран, Δs рассматривается именно на этом промежутке! Это было понятно, когда мы записывали аргументы функции s(t), но, вид записи изменился, и данный факт стал не столь очевиден.
Итак, повторим еще раз, что формула средней скорости приняла следующий вид:
vср = Δs/Δt
С учётом полученных нами знаний, формула для мгновенной скорости может быть записана так:
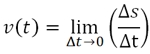
Читается это так: мгновенная скорость v(t) в некий момент времени t определяется, как предел отношения Δs/Δt при Δt стремящемся к нулю.
Обозначение lim (limes - предел) обозначает понятие предела, о котором было рассказано выше.
Внизу обязательно пишется о каком пределе идёт речь (в нашем случае, разинца времён стремится к нулю, т. е. две засечки времени располагаются как можно ближе друг к другу), стрелка заменяет слово "стремится"; в скобках указывается та величина, к которой ищется предел.
Все те "мытарства" по подобору как можно меньшего Δt для определения мгновенной скорости "на глазок", которые нами проводились на страницах График равномерного движения и График равноускоренного движения и есть понятием предела.
Приведем здесь одну из таблиц для графика движения s = t2, разобранных ранее:
t - s ------ 1 - 1 1,01 - 1,0201 1,1 - 1,21 1,5 - 2,25
Для t=1 мы проделали вычисления, результаты которых сведём в следующую таблицу:
Δt - Δs/Δt ---------- 0,5 - 2,5 0,1 - 2,1 0,01 - 2,01
С учётом знаний, полученных на этой странице, для t = 1 можно записать:
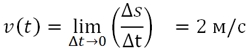
Дотошный читатель в этом месте может задать вполне логичный вопрос - а зачем столько "мучений" с многочисленными вычислениями, связанными с постепенным уменьшением Δt? Нельзя ли сразу в "дамки" - взять Δt=0?
Нет, нельзя, поскольку в таком случае мы бы не получили никакого перемещения, и при этом Δs/Δt = 0/0, а на ноль, как известно, делить нельзя.
Предел - это ведь такая "штука", к которой мы стремимся, но никогда не достигнем, ну, как "заветная и несбыточная мечта". Поэтому, Δ может быть сколь угодно малой величиной, но отличной от нуля - ведь, если не будет разницы во времени, то не будет никакого перемещения, поэтому, не будет и скорости, т.к. стоящее на месте тело не обладает никакой скоростью.
Из всего вышесказанного сделаем следующий важный вывод: при стремлении Δt к нулю, отношение Δs/Δt стремится к некоторому пределу (мгновенной скорости).
Предел отношения Δs/Δt получил название производной функции s(t).
Производная функции s(t) зависит от:
- вида функции s(t);
- значения переменной t.
В переводе на "простой язык", можно сказать, что производная показывает величину мгновенной скорости в некоторый момент времени t.
При помощи производной мы можем узнать скорость тела в любой момент времени, если нам известен закон (формула) движения этого тела.
