СКОРОСТЬ МЕХАНИЧЕСКОГО ДВИЖЕНИЯ
Скорость - векторная физическая величина, определяющая как быстроту движения, так и направление движения в данный момент времени.
Рассмотрим общий случай неравномерного криволинейного движения.
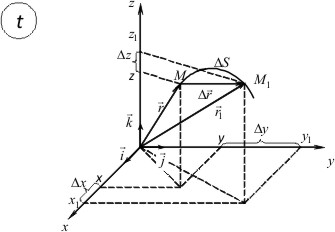
Рис. 1.2
Пусть в момент времени t движущееся точечное тело занимает положение M, характеризующееся радиус-вектором r или координатами x,y,z (рис. 1.2). К моменту времени t1=t+Δt тело займет новое положение M1 с r1 и координатами x1,y1,z1.
За отрезок времени Δt=t1-t , координаты движущегося тела изменяются на
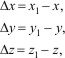(1.5)
а приращение радиус-вектора за это время будет равным: Δr=r1-r.
Проекции Δr на оси координат будут
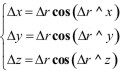
или вектор Δr выразиться через свои проекции следующим образом
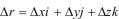(1.6)
где i,j,k - орты.
Величина вектора |Δr| будет равна
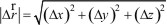(1.7)
Вектор Δr, направленный из начального положения M в конечное положение M1, движущегося в течение времени Δt точечного тела, называется вектором перемещения.
Расстояние между M и M1, отсчитанное вдоль траектории, называется путем ΔS, пройденным точкой. Путь ΔS - скалярная величина.
В общем случае криволинейного движения вектор Δr не совпадает с участком траектории ΔS, проходимым телом за соответствующий отрезок времени. В криволинейном движении ΔS>|Δr|.
Из того, что перемещение - вектор, следует подтверждающийся на опыте закон независимости движений: если точка одновременно участвует в нескольких движениях, то результирующее перемещение точки равно векторной сумме перемещений, совершаемых ею за то же время в каждом из движений порознь.
Если за время Δt радиус-вектор движущейся материальной точки изменяется на Δr, то среднее его изменение за 1 единицу времени будет (Δr/Δt).
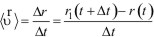(1.8)
Величина <v>, равная среднему изменению радиус-вектора материальной точки за единицу времени, называется средней скоростью ее перемещения за время между t и t+Δt. Она является величиной векторной, так как получается делением вектора Δr на скаляр Δt. Направление средней скорости <v> совпадает с направлением хорды 1,2, то есть с Δr.
В случае неравномерного движения с изменением Δt отклонение (Δr/Δt) будет изменяться, то есть
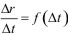
Следовательно, средняя скорость окажется неодинаковой при различных Δt, поэтому с ее помощью невозможно характеризовать движение в данный момент времени однозначно.
Посмотрим как будет изменяться Δr/Δt при уменьшении отрезка времени Δt (рис. 1.3). С течением времени точка непрерывно проходит через все точки своей траектории, при этом, чем меньше отрезок времени, тем меньший участок траектории проходит материальная точка. Так участок MM1 материальная точка проходит за время Δt, MM2 - Δt1, MM3 - Δt2, MM4 - Δt3, а векторы перемещений
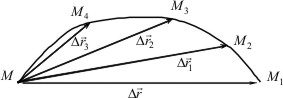
Рис. 1.3
соответствующие этим промежуткам времени соответственно Δr, Δr1, Δr2, Δr3. Эти векторы, как видно, уменьшаются с уменьшением Δt.
В пределе, когда отрезок, в течение которого рассматривается движение, неограниченно уменьшается, то есть когда Δt→0, вектор перемещения Δr по направлению совпадает с практически прямолинейным элементарно малым участком траектории и по величине окажется равным длине пути ΔS, проходимым за этот отрезок времени. Такое совпадение достигается всегда, если отрезок Δt достаточно мал. При этом данные элементарные участки траектории будут проходиться материальной точкой практически равномерно, поскольку состояние движения тела с течением времени может изменяться лишь непрерывно, так что для заметного его изменения требуется конечный, достаточно большой отрезок времени. Следовательно, если Δt мал, то с дальнейшим его уменьшением отношение Δr/Δt практически изменяться не будет ни по величине, ни по направлению. Иными словами, при Δt→0 отношение Δr/Δt стремится к определенному конечному предельному значению v, не зависящему от характера изменения Δt.
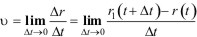(1.9)
Предел отношения приращения радиус-вектора движущейся материальной точки Δr к соответствующему отрезку времени Δt при условии, что Δt→0, называется производной от радиус-вектора r по времени t и обозначается r=dr/dt. Этот предел и будет скоростью движения точки в данный момент времени t - мгновенной скоростью.
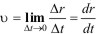(1.10)
Скорость движения материальной точки в данный момент времени есть производная ее радиус-вектора по времени.
Скорость, будучи величиной векторной, направлена так же, как и элементарно малый вектор перемещения, который в пределе при Δt→0 совпадает с элементарным участком траектории, то есть она направлена по касательной к траектории движущегося точечного тела в сторону движения.
Вектор скорости, как и любой другой вектор, имеет проекции на оси координат x,y,z соответственно vx,vy,vz и выражается через эти проекции таким образом
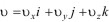(1.11)
где i,j,k - орты осей.
Проекции вектора скорости материальной точки на оси координат есть скорости движения проекций этой точки на данные оси, то есть они равны производным по времени от соответствующих координат движущейся точки.
Подставляя в (1.10) значение радиус-вектора r=xi+yj+zk и имея в виду, что производная суммы равна сумме производных от каждого слагаемого, а единичные векторы (орты) i,j,k с течением времени не изменяются ни по величине, ни по направлению, получим
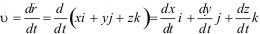
Вектор скорости v представляется в виде суммы трех взаимно перпендикулярных векторов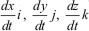 
, соответственно параллельных осям x,y,z. Учитывая, что проекция суммы векторов на направление, например, оси x, равна сумме проекций слагаемых векторов на это же направление, получим
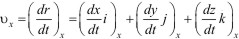(1.12)
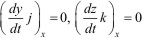, так как эти векторы перпендикулярны оси x.
Проекция же вектора (dx/dt)i на ось x равна длине данного вектора, dx/dt, так как величина вектора i равна единице. Аналогично получаем и для vy и vz. Таким образом, проекции вектора скорости на оси координат равны
; 
; 
,
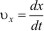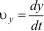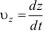а модуль скорости
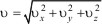(1.13)
При движении материальной точки по прямой в одном направлении пройденный путь и модули вектора перемещения совпадают ΔS=|Δr|.
Средней скоростью прохождения пути неравномерного движения материальной точки <v> на данном участке ее траектории называется скалярная величина, равная отношению длины пути ΔS ко времени Δt, за которое этот путь пройден.
Величину истинной скорости (без учета направления) можно определить таким образом. При Δt→0 длина |Δr| вектора перемещения в пределе совпадает с элементом пути ΔS, так что |Δr|/ΔS→1. С учетом этого величина скорости может быть представлена в виде
,
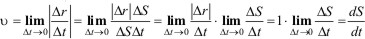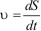, (1.14)
то есть величина скорости есть производная пути по времени.
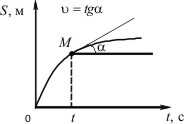
Рис. 1.4
Если дана графическая зависимость проходимого телом пути S от времени t, то величина скорости в данный момент времени будет равна tgα наклона касательной, проведенной в точке кривой S=f(t), соответствующей этому моменту времени и оси времени (рис. 1.4).
Зная модуль скорости в каждый момент времени, можно вычислить путь, пройденный частицей от t1 до t2
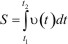, (1.15)
где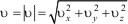 
.
