Нахождение закона движения тела по заданным ускорению и начальным условиям (ПРЯМАЯ ЗАДАЧА КИНЕМАТИКИ)
Рассмотрим прямую задачу кинематики, зная проекции ускорения тела ax, ay, az на оси координат как функции времени, определим зависимость координат данного тела от времени, то есть определим положение тела в пространстве в любой момент времени. Для этого необходимо знать еще и так называемые начальные условия, то есть координаты тела x0, y0, z0 в момент времени t=t0, а также проекции его начальной скорости v0x, v0y, v0z в тот же момент времени.
Итак, пусть известны: ax=ax(t) проекция ускорения материальной точки на ось x как функция времени, v0x - проекция на ось x начальной скорости, x0 - координата материальной точки в момент времени t0.
Найдем проекцию скорости этого тела vx на ось x и его координату x как функцию времени. То есть
vx=vx(t) - ?
x=x(t) - ?
Как известно, проекция ускорения на ось x равна
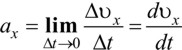
Производную dvx/dt можно понимать как отношение элементарно малого изменения проекции скорости dvx на ось x к соответствующему элементарно малому приращению времени dt. Но при этом величина dt должна быть настолько малой, что с ее дальнейшим уменьшением отношения dvx/dt практически уже изменяться не будет.
В силу сказанного можем соотношение ax=dvx/dt умножить на dt и получим: dvx=axdt - элементарно малое приращение скорости за малый отрезок времени dt.
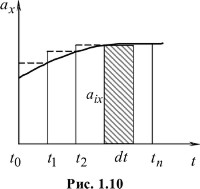
С учетом этого найдем изменение проекции скорости vx за конечный отрезок времени от начального t0 до t, для чего весь отрезок времени t-t0 разобьем точками t1, t2, t3...tn =t на n элементарных частей (рис. 1.10).
Если значения проекции скорости vx в моменты времени t1, t2, t3...tn обозначены условно через v0x, v1x, v2x...vx, то ее изменения за последовательно примыкающие друг к другу элементарные отрезки времени
……………
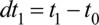
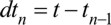
выразятся так
……………………………
,
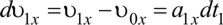
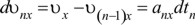где a1x, a2x...anx - значения проекций ускорения ax соответствующие отрезкам времени dt1, dt2, dt3...dtn.
Сложив эти равенства, получим
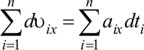
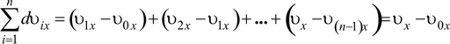, то есть получаем изменение скорости за весь промежуток времени t-t0.
Рассмотрим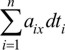 
. Каждое слагаемое aixdti равно площади прямоугольника с основанием dti и высотой aix. Вся сумма численно равна сумме площадей всех таких элементарных прямоугольников.
При dti→ ступенчатая линия сольется с кривой ax(t), таким образом, изменение скорости за время t-t0 будет равно площади фигуры, ограниченной кривой ax=ax(t), осью времени t и прямыми t=t0; t=tn.
Итак, переходя к пределу при dt1→0, получим
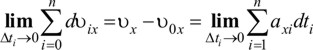
Предел суммы бесконечно большого числа бесконечно малых слагаемых, представляющих собой произведения значений функции ax(t) на соответствующие им приращения аргумента dt при условии, что dt1→0, называется интегралом данной функции. Тогда имеем
.
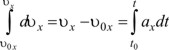Отсюда
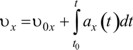
Таким же путем, зная зависимость проекции скорости тела на ось x от времени и координату x0 в начальный момент времени t0, можно определить координату тела x как функцию времени.
Известно, что vx=dx/dt, откуда dx=vxdt - изменение координаты x за элементарно малый отрезок времени dt.
Изменение координаты тела x за конечный отрезок времени t-t0 будет равно пределу суммы элементарных ее изменений, проходящих за все элементарные отрезки времени dti, составляющие конечный отрезок времени t-t0, при условии, что dti→0, то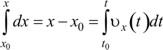 
, откуда 
.
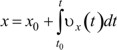Точно так же находятся проекции скорости тела на другие оси координат и сами координаты движущегося тела как функции времени.
