Скорость точки
Введем единичный вектор τ, связанный с движущейся точкой A и направленный по касательной к траектории в сторону возрастания дуговой координаты (рис. 1.6). Очевидно, что τ - переменный вектор: он зависит от l. Вектор скорости v точки A направлен по касательной к траектории, поэтому его можно представить так
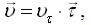(1.22)
где vτ=dl/dt - проекция вектора v на направление вектора τ, причем vτ - величина алгебраическая. Кроме того, |vτ|=|v|=v.
Ускорение точки
Продифференцируем (1.22) по времени
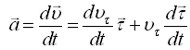(1.23)
Преобразуем последний член этого выражения
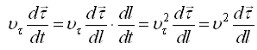(1.24)
Определим приращение вектора τ на dl (рис. 1.7).
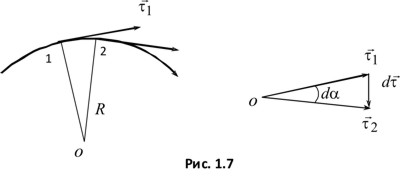
Как видно из рис. 1.7, угол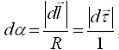 
, откуда 
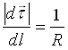, причем при 
.
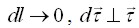Введя единичный вектор n нормали к траектории в точке 1, направленный к центру кривизны, запишем последнее равенство в векторном виде
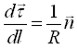(1.25)
Подставим (1.23) в (1.24) и полученное выражение в (1.22). В результате найдем
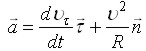(1.26)
Здесь первое слагаемое называют тангенциальным aτ, второе - нормальным an.
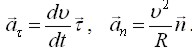
Таким образом, полное ускорение a точки может быть представлено как геометрическая сумма тангенциального и нормального ускорений.
Модуль полного ускорения точки
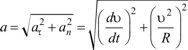(1.27)
Направлено оно в сторону вогнутости траектории под углом α к вектору скорости, причем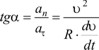 
.
Если угол α острый, то tgα>0, следовательно, dv/dt>0, так как v2/R>0 всегда.
В данном случае величина скорости возрастает с течением времени - движение называют ускоренным (рис. 1.8).
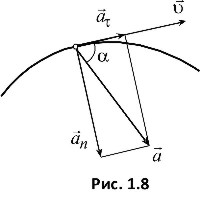
В том случае, когда скорость с течением времени уменьшается по величине, движение называется замедленным (рис. 1.9).
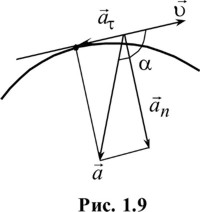
Если же угол α=90°, tgα=∞, то есть dv/dt=0. В этом случае скорость с течением времени по величине не изменяется, а полное ускорение будет равно центростремительному
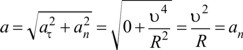(1.28)
В частности, полное ускорение равномерного вращательного движения (R=const, v=const) есть центростремительное ускорение, по величине равное an=v2/R и направленное все время к центру.
При прямолинейном движении, наоборот, полное ускорение тела равно тангенциальному. В данном случае an=0, так как прямолинейную траекторию можно считать окружностью бесконечно большого радиуса, а при R→∞; v2/R=0; an=0; a=aτ.
