График равномерного движения
Изучение производной начнём с детального рассмотрения равномерного поступательного движения материальной точки тела, которое будет описано при помощи функции.
Все желающие могут освежить свои знания о функции на странице "Что такое функция".
Пусть автомобиль марки "Лорен Дитрих" под названием "Антилопа Гну", ведомый Адамом Козлевичем, движется с постоянной скоростью (v) по шоссе от Козельска до Лучанска. Шоссе - это прямая линия, а расстояние, пройденное "Антилопой Гну" будем обозначать литерой s.
Расстояние s, пройденное автомобилем, будет меняться с течением времени (t).Словосочетание "расстояние s, пройденное автомобилем" заменим словосочетанием "координата s".
Когда "Антилопа-Гну" движется, её координата s меняется с течением времени t. На языке математики это будет звучать так:
Движение автомобиля определяется зависимостью его местоположения (координаты s) от времени t.
Другими словами - положение автомобиля в любой момент времени определено функцией s(t).
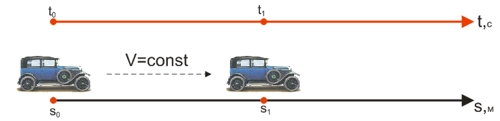
Функция s(t) может быть отображена графически на координатной плоскости:
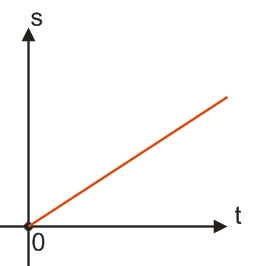
По оси ординат будем откладывать координату s автомобиля (пройденное им расстояние), а по оси абсцисс - время его движения t.
Графиком равномерного движения, как известно, является прямая. В нашем случае угол наклона такой прямой будет зависеть от скорости движения "Антилопы-Гну" - чем выше скорость движения, тем круче будет прямая.
Путь, пройденный автомобилем, движущимся с постоянной скоростью (v), за некоторое время t, можно вычислить по формуле:
s = vt
Дальше будем рассматривать перемещение автомобиля за некоторый отрезок времени t.
Пусть в начальный момент времени t=0 "Антилопа-Гну" имеет координату s0.
Через некоторое время t "Антилопа-Гну" переместится на некоторое расстояние и будет иметь новую координату s.
Путь, пройденный автомобилем за это время t, будет равен разности его координат в начальный момент времени и текущий момент:
s(t)-s0 или s(t) = s0+vt
Например, за 10 секунд, автомобиль, движущийся со скоростью 36 км/ч (10 м/с), переместится на расстояние в 100 м.
Всё вышесказанное должно быть предельно понятно и не вызвать каких-либо вопросов.
Теперь подойдём к движению автомобиля с постоянной скоростью с "другой стороны".
Предположим, что нам задана функция s(t) - мы знаем зависимость координаты автомобиля от времени (т. е. мы знамем, что в момент времени t1 координаты авто были s1, а в момент времени t2 - координаты s2).
Нам нужно найти скорость движения автомобиля v.
В случае равномерного движения данная задача вообще не вызывает никаких сложностей.
Скорость определяется, как расстояние, пройденное за определенный промежуток времени:
v=s/t
В случае равномерного движения не имеет значения какой участок пути или промежуток времени выбирать для определения скорости - скорость везде будет одинакова.
Пусть наша функция s(t) задана формулой (s - метры; t - секунды):
s=10t+10
В начальный момент времени: t=0; s=10.
Составим таблицу перемещения на первые 5 секунд движения:
t - s ------ 0 - 10 1 - 20 2 - 30 3 - 40 4 - 50 5 - 60
За первую секунду движения автомобиль пройдет расстояние:
s1-s0 = 20-10 = 10 м
Скорость движения авто в течение первой секунды движения:
v = 10/1 = 10 м/с
За вторую секунду движения автомобиль пройдет расстояние:
s2-s1 = 30-20 = 10 м
Скорость движения авто в течение второй секунды движения:
v = 10/1 = 10 м/с
За первые 5 секунд движения автомобиль пройдет расстояние:
s5-s0 = 60-10 = 50 м
Скорость движения авто в течение пяти секунд движения:
v = 50/5 = 10 м/с
Как видим, в случае равномерного движения автомобиля, не имеет никакого значения когда и где определять его скорость - везде она будет одинакова.
Совсем другая история получается, если автомобиль движется не с постоянной скоростью. Кому интересно, смотрите следующую страницу "График равноускоренного движения".
