Производная степенной функции
На странице Производная квадратичной функции достаточно подробно был изложен алгоритм поиска производной квадратичной функции алгебраическим путём.
В итоге была найдена формула производной квадратичной функции (y=x2):
y'=2x
Аналогичным способом найдем производные для других степенных функций, опуская при этом подробности.
Производная для функции y=x3
На первом этапе "избавляемся" от переменной y:
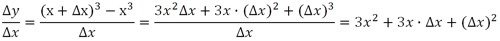
Находим предел:
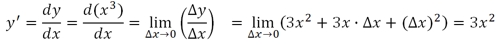
Производная для функции y=x4
На первом этапе "избавляемся" от переменной y:
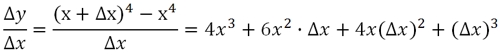
Находим предел:
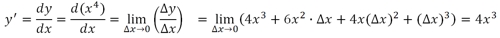
Искать производные для степенных функций с ещё большими натуральными степенями не имеет смысла. Уже понятно, что производная для степенной функции будет иметь вид:
| y=xn y'=n·xn-1 |
Производная для функции y=x-1
На первом этапе "избавляемся" от переменной y:
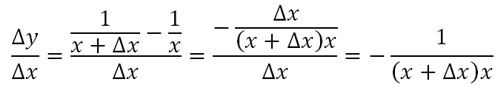
Для этого нам надо привести дроби к общему знаменателю.
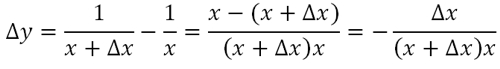
Находим предел:
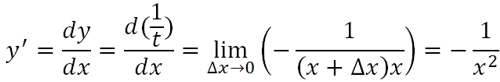
Производная для функции y=x-2:
y'=(x2)'=-2/x3
Как видим, найденная нами ранее формула производной степенной функции подходит и для отрицательных целых степеней.
Логично предположить, что она будет верна и для дробных степеней. Кто не верит, может проверить это самостоятельно. Проще всего это сделать для функции y=√x.
Подсказка: числитель и знаменатель выражения
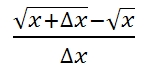
надо будет умножить на следующую сумму
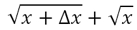
Для ленивых приводим решение:
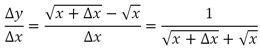
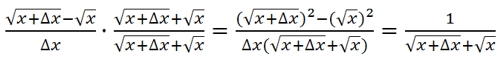
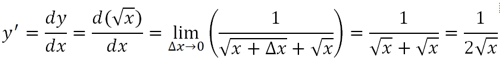
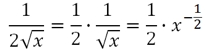
Напоследок обратим внимание на два частных случая.
Производная функции y=x
Для такой функции Δy=Δx.
Поэтому, Δy/Δx = 1 для любых Δx, следовательно и в пределе:
y=x dy/dx = dx/dx = 1
Еще одним частным случаем степенной функции является функция вида y=C, где С - число. Например, y=5.
Для этого случая очевидно, что Δy=0 при любых Δx:
y=С dy/dx = dС/dx = 0
