График равноускоренного движения
Предположим, что график движения автомобиля задан формулой:
s = t2
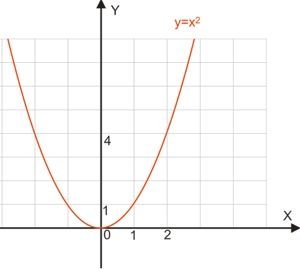
График, наверное, узнали все - это парабола. По оси X у нас откладывается время t; а по оси Y - перемещение s.
Составим таблицу перемещения автомобиля по аналогии с равномерным движением:
t - s ------ 0 - 0 1 - 1 2 - 4 3 - 9 4 - 16 5 - 25
За первую секунду движения автомобиль пройдет расстояние:
s1-s0 = 1-0 = 1 м
Скорость движения авто в течение первой секунды движения:
v = 1/1 = 1 м/с
За вторую секунду движения автомобиль пройдет расстояние:
s2-s1 = 4-1 = 3 м
Скорость движения авто в течение второй секунды движения:
v = 3/1 = 3 м/с
Мы видим, что за промежуток времени от первой до второй секунды скорость авто изменилась с 1 м/с до 3 м/с. Логично предположить, что скорость авто менялась и в промежутке времени от 0 до 1 секунды, и в промежутке от 1 секунды до 2 секунды. Таким образом, полученные значения скорости являются средними величинами.
А как узнать конкретную скорость в заданный момент времени? Такую скорость называют мгновенной скоростью (она отображается на спидометре автомобиля).
Свою скорость движения автомобиль меняет постепенно, поэтому, уменьшая промежуток времени, в течение которого будет производиться измерение пройденного пути, мы тем самым будем приближать среднюю скорость движения к мгновенной.
Возьмём три промежутка времени:
- от 1 секунды до 1,5 секунд;
- от 1 - до 1,1 секунды;
- от 1 - до 1,01 секунды.
Составим таблицу пройденного растояния:
t - s ------ 1 - 1 1,01 - 1,0201 1,1 - 1,21 1,5 - 2,25
Вычислим средние скорости для каждого из выбранных промежутков:
1-1,5 секунд v = (2,25-1)/(1,5-1) = 1,25/0,5 = 2,5 м/с 1-1,1 секунд v = (1,21-1)/(1,1-1) = 0,21/0,1 = 2,1 м/с 1-1,01 секунд v = (1,0201-1)/(1,01-1) = 0,0201/0,01 = 2,01 м/с
Как говорится, "невооруженным глазом" видно, что, чем меньше промежуток времени, отсчитываемый от 1 секунды, тем ближе скорость к 2 м/с.
Таким образом, можно предположить, что в момент времени 1 секунда после начала движения, мгновенная скорость автомобиля будет равна 2 м/с.
Проделаем тот же "фокус" с определением мгновенной скорости движения для момента времени t=2,5 секунды.
Составляем таблицу пройденного растояния:
t - s ------ 2,5 - 6,25 2,51 - 6,3001 2,6 - 6,76 3 - 9
Вычисляем средние скорости для каждого из выбранных промежутков:
2,5-3 секунд v = (9-6,25)/(3-2,5) = 2,75/0,5 = 5,5 м/с 2,5-2,6 секунд v = (6,76-6,25)/(2,6-2,5) = 0,51/0,1 = 5,1 м/с 2,5-2,51 секунд v = (6,3001-6,25)/(2,51-2,5) = 0,0501/0,01 = 5,01 м/с
Не надо быть "семи пядей во лбу", чтобы догадаться, что мгновенная скорость в момент времени 2,5 с будет равна 5 м/с.
ВНИМАНИЕ! Из всего вышеизложенного делаем архиважный вывод!!!
|
Мгновенная скорость есть функция времени t. v=v(t) |
Всё очень просто, - мы увидели, что с течением времени скорость автомобиля меняется, точно так же, как и меняется пройденное им расстояние.
В приведённых выше примерах мы приближались к выбранному моменту времени с одной "стороны". Можно это делать с "обеих сторон", тогда значение мгновенной скорости можно вычислить совершенно точно, как среднее арифметическое (но это можно сделать только в случае равноускоренного движения).
Берём следующие промежутки времени:
- 0,9-1 с;
- 0,99-1 с;
- 1-1,01 с;
- 1-1,1 с.
Составляем таблицу пройденного растояния:
t - s ------ 1 - 1 1,01 - 1,0201 1,1 - 1,21 0,9 - 0,81 0,99 - 0,9801
Вычисляем средние скорости для каждого из выбранных промежутков:
0,9-1 секунд v = (1-0,81)/(1-0,9) = 0,19/0,1 = 1,9 м/с 1-1,1 секунд v = (1,21-1)/(1,1-1) = 0,21/0,1 = 2,1 м/с 0,99-1 секунд v = (1-0,9801)/(1-0,99) = 0,0199/0,01 = 1,99 м/с 1-1,01 секунд v = (1,0201-1)/(1,01-1) = 0,0201/0,01 = 2,01 м/с
Теперь берем "зеркальные" промежутки времени "влево" и "вправо" от 1 секунды, и вычисляем среднее арифметическое:
0,9-1 и 1-1,1 (1,9+2,1)/2 = 2 м/с 0,99-1 и 1-1,01 (1,99+2,01)/2 = 2 м/с
Поздравляю, мы вплотную подошли к определению производной (см. Производная функции).
