Производная квадратичной функции
На странице "Производная функции" мы выяснили, что предел отношения Δs/Δt получил название производной функции s(t).
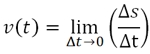
Напомним, что величина Δs - это приращение расстояния; Δt - приращение времени.
Определение производной можно сформулировать в следующем виде:
Производной называется предел отношения приращения расстояния к приращению времени, при стремлении к нулю последнего.
Если уйти от конкретики, и не привязываться к расстоянию и времени, то определение производной будет звучать так:
Производная - это предел отношения приращения функции к приращению независимой переменной при стремлении к нулю приращения независимой переменной.
Смысл производной заключается в том, что она показывает скорость изменения функции при изменении её аргумента.
Напомним важные моменты производной для функции s(t):
- приращение независимой переменной может быть сколь угодно малым, но обязательно отличным от нуля;
- поскольку s есть функция t [s(t)], то и предел отношения Δs/Δt является также функцией t, которая называется мгновенной скоростью v(t);
- v зависит от значения t при котором берется производная s.
Обозначение производной через предел довольно громоздко и не совсем удобно, поэтому, чаще используют сокращенные варианты (в общем случае вместо переменной s используется перменная y, а вместо переменной t - переменная x - что вполне логично, поскольку расстояние мы откладывали по оси ординат, а время - по оси абсцисс):
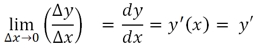
Частенько вместо функции пишется ее выражение:
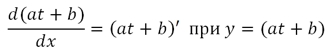
На странице Равноускоренное движение мы искали производную квадратичной функции "наощупь", пошагово уменьшая приращение времени, теперь сделаем это алгебраически.
Изначально составим соотношение:
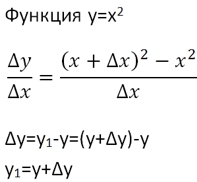
Знаменатель не трогаем. В числителе делаем преобразования, чтобы избавиться от переменной y. Дэльта игрек - это разность между начальной точкой (y) и некой точкой (y1), соответствующей величине приращения (y+Δy). После этого заменяем y на x2.
Раскрывая скобки в числителе, получаем выражение:
(x+Δx)2-x2=x2+2x·Δx+(Δx)2-x2 2x·Δx+(Δx)2
Теперь наше соотношение примет следующий вид:
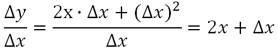
Ищем предел квадратичной функции:
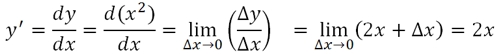
Последнее равенство требует пояснения. Предел двух слагаемых одно из которых независимо, а второе стремится к нулю, будет равен независимому слагаемому.
Алгебраическим путём мы нашли производную квадратичной функции (y=x2):
y'=2x
Теперь ещё раз вернёмся на страницу Равноускоренного движения, на которой мы пошаговым путём нашли производную квадратичной функции для значений t=1 (s'=2) и t=2,5 (s'=5).
Подставляя эти же значения в нашу формулу, мы получим те же значения производных.
