Приближенное вычисление функции с помощью производной
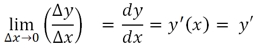
Производная dy/dx есть предел отношения приращения функции (Δy) к приращению её независимой переменной (Δx), когда последняя стремится к нулю.
Для лучшего понимания материала будем рассматривать функцию расстояния от времени s(t).
Следует понимать, что, чем меньше промежуток времени Δt, тем ближе отношение приращений Δs/Δt к производной функции ds/dt, поэтому, при достаточно малых значениях Δt можно считать Δs/Δt ≈ ds/dt.
Алгебраически это можно записать следующим образом:

Отсюда:

Приближенное значение функции s(t+Δt)
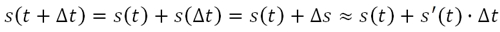
Сделаем подстановку Δt = (t1-t0), тогда функция s(t1) может бытть выражена приближенной формулой, которая будет включать значение функции s(t0) и её производной s'(t0) при t0=t:
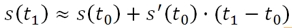
Обратите внимание, что приращённый аргумент t1, входит в эту формулу в первой степени, т. е., линейно.
В этом месте читатель резонно может заметить, - а зачем весь этот непонятный "огород" с подстановками и приближенными равенствами?
Минутку терпения. Переходим ко второй части Марлезонского балета, т.е., разбираем теорию на примерах.
Возьмём степенную функцию s=t4, и вычислим значения s в момент времени, близком к t=2.
s=t4; t=2 t0=t s(t0)=t04=24=16 s'(t0)=4t03=4·23=32
Приближенная формула:
s(t1)=t14≈16+32(t1-2)=32t1-48
Вычислим точное и приближенное значение функций для различных Δt и полученные данные сведём в таблицу:
| t1 | t14 | 32t1-48 |
|---|---|---|
| 2 | 16 | 16 |
| 2,01 | 16,322 | 16,320 |
| 2,05 | 17,661 | 17,60 |
| 2,1 | 19,448 | 19,2 |
| 2,5 | 39,0625 | 32 |
| 3 | 81 | 48 |
Проведем аналогичные расчёты для другой функции s=1/t.
s=t-1; t=2 t0=t s(t0)=t0-1=2-1=1/2 s'(t0)=-t0-2=-1·2-2=-1/4
Приближенная формула:
s(t1)=t1-1≈(1/2)-(1/4)(t1-2)=1-t1/4
| t1 | 1/t1 | 1-t1/4 |
|---|---|---|
| 2 | 0,5 | 0,5 |
| 2,01 | 0,49751 | 0,49750 |
| 2,05 | 0,4878 | 0,4875 |
| 2,1 | 0,476 | 0,475 |
| 2,5 | 0,400 | 0,375 |
| 3 | 0,33 | 0,25 |
Напомним, что мы рассматривали функцию s(t), где Δt - промежуток времени; s'(t) - мгновенная скорость; Δs - расстояние, пройденное за Δt, т. е., приращение пути.
Формула Δs=s'(t)Δt показывает расстояние, пройденное телом за выбранный промежуток времени. Нюанс заключается в том, что сама производная (мгновенная скорость) также меняется во времени (в случае, если движение не равномерное). Поэтому, путь, рассчитанный по указанной формуле, будет тем ближе к истинному, чем меньший промежуток времени рассматривается. Здесь всё логично, если скорость меняется, то за меньший промежуток времени она изменится на меньшее значение, следовательно, рассчёт пути будет более точным. Данный факт наглядно прослеживается в обеих таблицах, приведенных выше. Для первой функции погрешность для Δt=0,01 составляет 0,002, а для Δt=1 - уже 33.
Ещё один важный момент - величина изменения мгновенной скорости зависит не только от Δt, но и от конкретной функции, что также наглядно прослеживается в вышеприведенных таблицах. Для первой функции при Δt=1 разница в вычислениях составляет примерно 40% (показания 81 и 48), тогда, как для второй - только 25% (показания 0,33 и 0,25). Это значит, что для второй функции при определенной степени допустимой погрешности можно брать более длинные промежутки времени, нежели для первой.
Примеры приближенного вычисления функций с помощью производной
Пример 1.Найти с помощью производной приближенное значение 1,22.
Решение.
y=x2=1,22 x=1,2; x0=1, Δx=0,2 x=x0+Δx; 1,2=1+0,2
Формула для приближенного вычисления:
y(x)=y(x0+Δx)≈y(x0)+y'(x0)Δx y(1,2)=y(1+0,2)≈y(1)+y'(1)·0,2
Вычисляем первое слагаемое:
y(x0)=y(1)=12=1
Вычисляем первый множитель второго слагаемого:
y'(x0)=(x02)'=2x0 y'(1)=2·1=2
Вычисляем второе слагаемое:
y'(x0)Δx=2·0,2=0,4
Подставляем полученные данные в формулу для приближенного вычисления:
y(x)≈y(x0)+y'(x0)Δx y(1,2)≈1+0,4=1,4
Сравниваем с реальным значением:
1,22=1,44 y(1,2)≈1,4
Почему в качестве значения для x0 была взята единица? Чисто из меркантильных соображений - с одной стороны, 1 достаточно близка к 1,2, а с другой - с единицей очень легко проводить арифметические действия. Если бы для x0 было выбрано значение, например, 1,1, то погрешность получилась бы меньше, а если бы, например, 1,5 - то больше.
Пример 2. Найти с помощью производной приближенное значение 6001/4.
В этом случае для значения x0 логично выбрать число 625, т.к. корень четвёртой степени из 625 будет 5.
Решение.
y=x1/4=6001/4 x=600; x0=625, Δx=-25 x=x0+Δx; 625=600+(-25)
Формула для приближенного вычисления:
y(x)≈y(x0)+y'(x0)Δx y(600)=y(625-25)≈y(625)+y'(625)·(-25)
Вычисляем первое слагаемое:
y(x0)=y(625)=6251/4=5
Вычисляем первый множитель второго слагаемого:
y'(x0)=(x01/4)'=(1/4)·(x0-3/4) y'(625)=(1/4)·(1/125)=1/500
Вычисляем второе слагаемое:
y'(x0)Δx=(1/500)·(-25)=-1/20=-0,05
Подставляем полученные данные в формулу для приближенного вычисления:
y(x)≈y(x0)+y'(x0)Δx y(600)≈5+(-0,05)=4,95
Сравниваем с реальным значением:
6001/4=9,949 y(600)≈4,950
Пример 3.Найти с помощью производной приближенное значение функции x2+√x для точки х=1,21.
Решение.
y=x2+√x=1,212+√1,21=2,5641 x=1,21; x0=1, Δx=0,21 x=x0+Δx; 1,21=1+0,21
Формула для приближенного вычисления:
y(x)=y(x0+Δx)≈y(x0)+y'(x0)Δx y(1,21)=y(1+0,21)≈y(1)+y'(1)·0,21
Вычисляем первое слагаемое:
y(x0)=y(1)=12+√1=2
Вычисляем первый множитель второго слагаемого:
y'(x0)=(x02+√x0)'=2x0+1/(2·√x0) y'(1)=2·1+1/(2·√1)=2,5
Вычисляем второе слагаемое:
y'(x0)Δx=2,5·0,21=0,525
Подставляем полученные данные в формулу для приближенного вычисления:
y(x)≈y(x0)+y'(x0)Δx y(1,2)≈2+0,525=2,525
Сравниваем с реальным значением:
2,5641 2,5250
Пример 4.Найти с помощью производной приближенное значение tg(41°).
Решение.
Чтобы решить поставленную задачу, необходимо градусы перевести в радианы. Учитывая, что tg(45°)=1, для x0 выберем значение 45°.
y=tg(x)=tg(41°)=0,87 x=41°; x0=45°, Δx=-4° x=x0+Δx; 41°=45°-4° x0=π/4, Δx=(-4°π/180)=-π/45
Формула для приближенного вычисления:
y(x)=y(x0+Δx)≈y(x0)+y'(x0)Δx
Вычисляем первое слагаемое:
y(x0)=y(π/4)=tg(π/4)=1
Вычисляем первый множитель второго слагаемого:
y'(x0)=(tg(x0))'=1/cos2(x0) y'(π/4)=1/cos2(π/4)=1/(√2/2)2=2
Вычисляем второе слагаемое:
y'(x0)Δx=2·(-π/45)=-π/22,5≈0,14
Подставляем полученные данные в формулу для приближенного вычисления:
y(x)≈y(x0)+y'(x0)Δx tg(41°)≈1-0,14=0,86
Сравниваем с реальным значением:
0,87 0,86
