Что такое синус, косинус, тангенс, котангенс
Рассмотрим окружность, центр которой совпадает с центром координат, а радиус равен ОА:
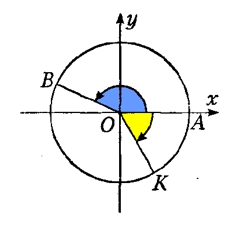
Повернув радиус ОА против часовой стрелки, получим некий угол АОВ. Такой угол называется положительным (на рисунке выделен синим цветом).
Повернув радиус ОА по часовой стрелке, получим угол АОК. Такой угол называется отрицательным (на рисунке выделен желтым цветом).
Теперь возьмем некий положительный угол АОВ, полученный поворотом радиуса ОА против часовой стрелки на некоторый угол α (закрашен желтым цветом):
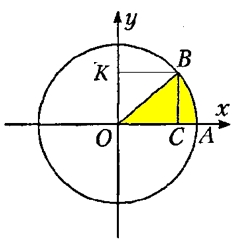
Синусом угла AOB (или α) называют отношение ординаты точки В (отрезок ОК=ВС) к длине радиуса ОВ:
sin AOB = ВC/OB sin α = ВC/OB
Косинусом угла AOB (или α) называют отношение абсциссы точки В (отрезок ОС) к длине радиуса ОВ:
cos AOB = ОC/OB cos α = ОC/OB
Тангенсом угла АОВ называют отношение синуса этого угла к его косинусу:
tg α = (sin α)/(cos α)
Котангенсом угла АОВ называют отношение косинуса этого угла к его синусу:
ctg α = (cos α)/(sin α)
Поскольку, в формулах тангенса и котангенса присутствует деление, то тангенс и котангенс не всегда можно определить, поскольку на ноль делить нельзя.
Тангенс угла невозможно определить, когда косинус этого угла принимает нулевое значение, - это все углы 90°+180°·n или π/2+π·n, где n-любое целое число.
Котангенс угла невозможно определить, когда синус этого угла принимает нулевое значение, - это все углы 0°+180°·n или π·n, где n-любое целое число.
Нетрудно заметить, что рассматриваемый нами угол α, является центральным острым углом прямого треугольника СОВ - его вершина совпадает с началом координат, а величина меньше 90°. При этом, один из катетов (ОС) треугольника СОВ расположен на оси абсцисс.
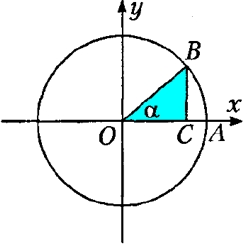
В таком случае, противоположный углу α катет ВС является ординатой лежащей на окружности вершины В, а прилежащий катет ОС - абсциссой вершины В, при этом гипотенуза ОВ будет радиусом окружности.
Учитывая изложенное обстоятельство, определения синуса, косинуса, тангенса и котангенса угла α прямоугольного треугольника СОВ будут формулироваться следующим образом:
- Синусом угла α (sin α) называют отношение противолежащего к углу α катета к гипотенузе: ВС/ОВ;
- Косинусом угла α (cos α) называют отношение прилежащего к углу α катета к гипотенузе: ОС/ОВ;
- Тангенсом угла α (tg α) называют отношение противолежащего к углу α катета к прилежащему: ВС/ОС;
- Котангенсом угла α (ctg α) называют отношение прилежащего к углу α катета к противолежащему: ОС/ВС;
Обратите внимание на важное обстоятельство - тригонометрические величины sin, cos, tg, ctg не зависят от величины радиуса окружности (длины гипотенузы прямоугольного треугольника), а зависят только от величины угла α. Поэтому, в тригонометрии считают, что рассматриваемый угол α является центральным углом окружности с радиусом, равным условной единице (так называемая окружность с единичным радиусом): r=1.
В таком случае, для вершины В, расположенной на окружности с единичным радиусом, можно сказать, что:
sin α = YB cos α = XB tg α = YB/XB ctg α = XB/YB
Следует запомнить значения синуса, косинуса, тангенса и котангенса для "стандартных" углов, которые будут встречаться наиболее часто в дальнейшем:
- α = 0°
sin α = 0 cos α = 1 tg α = 0 ctg α - не существует
- α = 30°(π/6)
sin α = 1/2 cos α = √3/2 tg α = √3/3 ctg α = √3
- α = 45°(π/4)
sin α = √2/2 cos α = √2/2 tg α = 1 ctg α = 1
- α = 60°(π/3)
sin α = √3/2 cos α = 1/2 tg α = √3 ctg α = √3/3
- α = 90°(π/2)
sin α = 1 cos α = 0 tg α - не существует ctg α = 0
