Свойства тригонометрических функций
Как определить знак синуса, косинуса
Работая с тригонометрическими функциями, очень важно понимать и знать где и как та или иная функция меняет свой знак.
Для этого знать, что из себя представляют координатные четверти:

Рассматриваемый угол α - это центральный угол, полученный поворотом радиуса единичной окружности (см. Что такое синус).
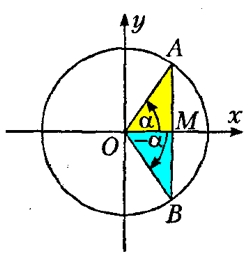
- знак синуса угла АОМ совпадает со знаком ординаты точки М (YM)
- знак косинуса угла АОМ совпадает со знаком абсциссы точки М (ХM)
- знаки тангенса и котангенса угла АОМ совпадают со знаком отношения синуса и косинуса этого угла.

Заучивать наизусть знаки тригонометрических функций в соответствующих квадрантах не имеет смысла. Достаточно начертить тригонометрический круг и отложить нужный угол (напомним, что положительное направление отсчитывается против часовой стрелки). Если конец подвижного радиуса расположен выше оси абсцисс (оси Х), то синус угла будет положителен; если ниже - отрицателен. Если конец подвижного радиуса расположен правее оси ординат (оси Y), то косинус угла будет положителен; если левее - отрицателен. Знак тангенса и котангенса устанавливается по фактическому значению знака синуса и косинуса.
Четные и нечетные функции
Синус, тангенс и котангенс являются нечетными функциями:
sin (-α) = -sin α tg (-α) = -tg α ctg (-α) = -ctg α
Косинус - четная функция:
cos (-α) = cos α
Это хорошо видно, если на тригонометрическом круге начертить два одинаковых, но разнонаправленных угла (желтый и синий):

На рисунке видно, что углы α и -α имеют одинаковое значение абсциссы (Х), т.е., косинусы одинаковых, но разнонаправленных углов будут равны.
Периодичность функций
Тригонометрические функции - это периодические функции, поскольку значение этих функций повторяется через определенный период, или, говоря другими словами, существуют определенные числа, прибавление которых к углу, не изменяет значение функции этого угла.
Для синуса и косинуса наименьшим периодом является значение 2π (360°), для тангенса и котангенса - это значение в два раза меньше: π (180°).
Понять это очень просто, если опять же обратиться к тригонометрическому кругу. Начертив полную окружность круга, мы снова попадем в исходную точку, т.е., значение синуса и косинуса углов 0° и 360° будут одинаковы, поскольку, на круге это будет одна и та же точка.
Чтобы найти значение функции, аргумент которой превышает 360° (2π), надо вычесть целое число периодов, укладывающихся в аргумент:
cos 560° = cos (560°-360°) = cos 200° sin 5π = sin (5π-4π) = sin π
Решим задачу посложнее, отыскав наименьший период для функции y=sin(x+1/2π).
Пусть k - наименьший период рассматриваемой функции, прибавление которого к исходному аргументу х, значение функции не изменит:
sin((x+k)+1/2π) = sin(x+1/2π)
Будем рассматривать аргумент (x+1/2π), как единое целое. В таком случае, наименьшим периодом будет значение 2π:
sin((x+2π)+1/2π) = sin(x+1/2π)
Теперь можно найти наименьший период для нашей задачи:
sin((x+2π)+1/2π) = sin((x+k)+1/2π) (x+2π)+1/2π = (x+k)+1/2π x+2,5π = x+k+0,5π k=2π
