Формулы приведения углов
Следует сразу оговориться, что данная тема весьма сложна для понимания. Для того, чтобы было легче вникнуть в суть принципа приведения углов, надо каждый случай рассматривать через графическое изображение тригонометрического круга, на котором следует откладывать углы - такая наглядность в значительной мере облегчит усвоение материала.
Формулы приведения позволяют выразить тригонометрические функции углов вида: π/2+α, π+α, 3π/2+α, 2π+α через тригонометрические функции угла α.
Зачем нужны формулы приведения?
Формулы приведения позволяют привести запись тригонометрической функции угла, величина которого лежит в пределах 0-90° (0-π/2) - первый квадрант, в котором и синус, и косинус положительны, что дает возможность с одной стороны значительно упростить последующие вычисления и упрощения, а с другой - быстро найти табличные значения угла.
Например, cos(530°) через формулы приведения можно преобразовать следующим образом:
cos(2π+π/2+80°) = -sin(80°)
На чем основан принцип формул приведения?
Первое, что надо всегда помнить, - в тригонометрии все углы имеют цикличность в 2π (360°) - т. е., значения всех тригонометрических функций углов, кратных 2π будут одинаковы:
- sin(20°)=sin(380°)=sin(740°) и т.д.
- cos(20°)=cos(380°)=cos(740°) и т.д.
- tg(20°)=tg(380°)=tg(740°) и т.д.
- ctg(20°)=ctg(380°)=ctg(740°) и т.д.
Но, кроме этого, такие тригонометрические функции угла, как синус и косинус, изменяясь в диапазоне от -1 до +1, в зависимости от величины угла, носят цикличный характер, поэтому, величины тригонометрических функций различных углов, лежащих в диапазоне от 0 до 2π могут быть равны.
Например:
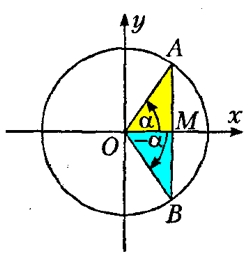
Из рисунка очень хорошо видно, что абсциссы углов α (AOM) и -α (ВOM) равны, следовательно cos(α)=cos(-α).
Но, угол -α (ВOM), можно представить, как 2π-α, поэтому, cos(2π-α)=cos(α).
Формулы приведения для синуса
sin(π/2-α) = cos(α) sin(π/2+α) = cos(α) sin(π-α) = sin(α) sin(π+α) = -sin(α) sin(3π/2-α) = -cos(α) sin(3π/2+α) = -cos(α) sin(2π-α) = -sin(α) sin(2π+α) = sin(α)
Формулы приведения для косинуса
cos(π/2-α) = sin(α) cos(π/2+α) = -sin(α) cos(π-α) = -cos(α) cos(π+α) = -cos(α) cos(3π/2-α) = -sin(α) cos(3π/2+α) = sin(α) cos(2π-α) = cos(α) cos(2π+α) = cos(α)
Формулы приведения для тангенса
tg(π/2-α) = ctg(α) tg(π/2+α) = -ctg(α) tg(π-α) = -tg(α) tg(π+α) = tg(α) tg(3π/2-α) = ctg(α) tg(3π/2+α) = -ctg(α) tg(2π-α) = -tg(α) tg(2π+α) = tg(α)
Формулы приведения для котангенса
ctg(π/2-α) = tg(α) ctg(π/2+α) = -tg(α) ctg(π-α) = -ctg(α) ctg(π+α) = ctg(α) ctg(3π/2-α) = tg(α) ctg(3π/2+α) = -tg(α) ctg(2π-α) = -ctg(α) ctg(2π+α) = ctg(α)
Запомнить все формулы приведения достаточно непросто, ибо в них не прослеживается какой-либо явной закономерности.
Однако, это можно сделать, если понять принцип по которому в приведенной формуле происходит или не происходит смена функции на кофункцию и смена или не смена знака функции.
Когда надо менять название функции в формуле приведения?
Смена или не смена функции в формуле приведения зависит от того, к какому диаметру тригонометрического круга прилежит угол α в формуле приведения.
π/2±α и 3π/2±α - это вертикальный диаметр тригонометрического круга (ось Y), поскольку точки π/2 и π3/2 лежат на оси Y. Если помотать головой вверх-вниз, как бы скользя взглядом по оси ординат, то автоматически получим ответ на вопрос "надо ли менять название функции в формуле приведения?" - да, надо.
π±α и 2π±α - это горизонтальный диаметр тригонометрического круга (ось X), поскольку точки π и 2π лежат на оси Х. Если помотать головой влево-вправо, как бы скользя взглядом по оси абсцисс, то автоматически получим ответ на вопрос "надо ли менять название функции в формуле приведения?" - нет, не надо.
Когда надо менять знак функции в формуле приведения?
Для ответа на этот вопрос надо знать знаки функций синуса, косинуса, тангенса и котангенса в каждом квадранте тригонометрического круга.

Для синуса и косинуса - это просто, если помнить, что синус - это ордината (Y), а косинус - абсцисса (X):
- sin - это ось Y или вертикальная ось, поэтому, все, что лежит выше оси абсцисс - это "плюс" (I, II квадранты), что лежит ниже - "минус" (III, IV квадранты);
- cos - это ось X или горизонтальная ось, поэтому, все, что лежит правее оси ординат - это "плюс" (I, IV квадранты), что лежит левее - "минус" (II, III квадранты);
- tg и ctg - это отношение синуса и косинуса, поэтому, тангенс и котангенс будут положительны в тех квадрантах, в которых синус и косинус имеют одинаковый знак - это нечетные квадранты (I, III); соответственно, в четных квадрантах тангенс и котангенс будут отрицательны.
Знак функции в формуле приведения ставится по квадранту исходного угла, при этом считаем, что сам угол α является острым.
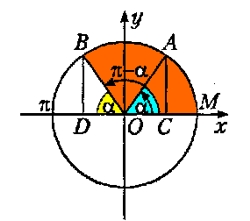
Например, для угла π-α получается, что угол находится во II квадранте, т.к., π-α будет лежать в пределах от 90° до 180° (см. рисунок выше). Во втором квадранте синус положителен, поэтому, в формуле приведения надо будет ставить знак, идентичный знаку исходной функции, т. е., "плюс". Поскольку угол π-α прилежит к горизонтальному диаметру, то сама функция не меняется. Получается, что sin(π-α) = sin(α).
Для косинуса надо будет сменить знак, т.к., во втором квадранте косинус отрицателен: cos(π-α) = -cos(α).
Для тангенса и котангенса: в четном квадранте - знак "минус", а функция остается прежней: tg(π-α) = -tg(α); ctg(π-α) = -сtg(α).
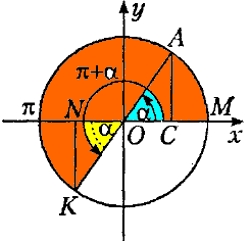
Для угла π+α получается, что угол находится во III квадранте, т.к., π+α будет лежать в пределах от 180° до 270° (см. рисунок). В третьем квадранте синус отрицателен, поэтому, в формуле приведения надо будет сменить знак. Поскольку угол π+α прилежит к горизонтальному диаметру, то функция не меняется. Получается, что sin(π+α) = -sin(α). Аналогично для косинуса: cos(π+α) = -cos(α).
Для тангенса и котангенса: в нечетном квадранте - знак "плюс", а функция остается прежней: tg(π+α) = tg(α); ctg(π+α) = сtg(α).
Десятиминутный ролик на ЮТуб, посмотрев который, вы навсегда запомните, как легко и просто приводить углы в тригонометрических функциях:

Пример решения уравнения с помощью формул приведения:
√2·sin(13π/4) √2·sin(3π+π/4) √2·sin(π+π/4) sin(π+π/4)=-sin(π4)=-√2/2 √2·(-√2/2)=-1
