Отрезок, луч, прямая
Раздел математики, изучающий объемные фигуры и законы их измерения, называется геометрией.
Планиметрия изучает двумерные фигуры, расположенные на плоскости.
Любая фигура, будь она объемной, плоскостной или линейной, состоит из множества точек - таких себе математических аналогов атомов реального мира.
Простейшими фигурами планиметрии являются отрезок, луч и прямая.
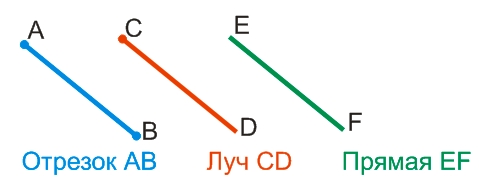
Всё это прямые линии, главное отличие которых друг от друга заключается в следующем:
- прямая не имеет ни начала, ни конца;
- луч имеет начало, но не имеет конца;
- отрезок имеет начало и конец.
Важно понимать, что математическая прямая, луч или отрезок не имеют такого понятия, как толщина - это прямые линии, состоящие из совокупности точек, стоящих "плечом к плечу" рядом друг с другом. Математическая точка не имеет никакой размерности - она может характеризоваться только координатами.
Провести "настоящую" прямую или луч невозможно, поэтому, ограничиваются построением отрезка, а чтобы различать отрезок, луч и прямую, ставят или не ставят точку в начале и конце отрезка:
- отрезок с обеих сторон ограничивается точками;
- у луча точка ставится в его начале;
- прямая точками не ограничивается.
Совпадающие прямые
Две прямые, расположенные в одной плоскости, могут либо пересекаться друг с другом (иметь одну общую точку), либо не пересекаться друг с другом (не иметь общих точек).
Возьмем произвольные четыре точки A, B, C, D, расположенные в одной плоскости и лежащие на одной прямой.
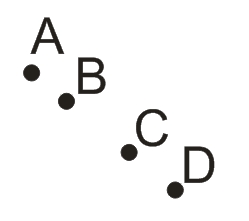
Проведем одну прямую через точки A и D, а вторую прямую - через точки В и С.
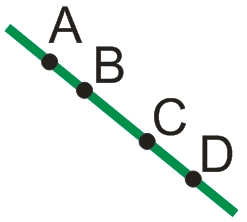
Очевидно, что вторая прямая наложится на первую. Говорят, что прямые AD и BC совместились или совпали.
Совпадающие прямые не являются ни пересекающимися, ни параллельными, поскольку имеют бесконечное множество общих точек. Все же, некоторые авторы совмещенные прямые рассматривают, как частный случай параллельных прямых, что, в общем-то, недалеко от истины.
Скрещивающиеся прямые
Две прямые, имеющие одну общую точку, называются скрещивающимися.
Частный случай скрещивающихся прямых - перпендикулярные прямые.
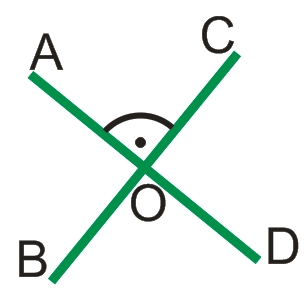
Перпендикулярными прямыми называются две скрещивающиеся прямые, при пересечении которых образуются четыре прямых угла.
Чтобы сделать вывод являются ли скрещивающися прямые перпендикулярными, достаточно знать величину одного из четырех углов, которые образуют скрещивающиеся прямые - если любой из таких углов равен 90°, то и все три остальных будут также равны 90°, т. е., прямые будут перпендикулярными. Если же какой-либо из углов не равен 90°, то ни один из углов не будет равен 90°, а, значит, такие прямые не будут перпендикулярными.
Доказать это очень просто.
При пересечении двух прямых образуются 4 угла (см. рисунок выше): AOC, COD, DOB, BOA.
Если один из углов, например, АОС, равен 90°, то и смежный с ним угол COD также будет равен 90° (см. Что такое угол). Также будет прямым и другой смежный угол BOA.
Углы AOC и DOB также будут равны между собой, поскольку являются вертикальными углами.
Если же, какой-либо из углов (например, угол АОС) не является прямым, то прямыми не будут и смежные с ним углы COD и BOA. Поскольку, углы AOC и DOB являются вертикальными, то они равны между собой, а, т. к., угол АОС не равен 90°, то и угол DOB также не будет прямым.
Свойство перпендикулярных прямых: через любую точку плоскости можно провести тлько одну прямую, перпендикулярную данной прямой.
Параллельные прямые
Прямые будут параллельными, если они не имеют общих точек и при этом лежат в одной плоскости.
Аксиома параллельных прямых: через любую точку плоскости можно провести тлько одну прямую, параллельную данной прямой.
