Что такое физика?
- Как мы измеряем мир? Системы измерения
- Экспоненциальное представление чисел
- Точность измерений
- Немного алгебры и тригонометрии
Физика - это модель нашего мира.
Суть физики бегло можно выразить так: Наблюдение → Создание модели → Математическое описание
Физика и математика - "неразлей-друзья". Однако, всегда надо помнить, что сначала реальный мир, а математика уже потом.
1. Как мы измеряем мир? Системы измерения
Измерение - вот начальная точка физики!
Исторически сложилось так, что существует множество мер одного и того же параметра: длины, веса, времени… Чтобы не запутаться во всем этом многообразии, физики и математики сгруппировали меры в системы единиц измерения. Наиболее известные системы измерения: СИ (система интернациональная) и СГС (сантиметр-грамм-секунда).
Ниже представлены основные единицы измерения в этих системах:
| Параметр | СИ | СГС |
|
Длина Масса Время Сила Энергия Давление Эл.ток Маг.индукция Эл.заряд |
метр (м) килограмм (кг) секунда (с) ньютон (Н) джоуль (Дж) паскаль (Па) ампер (А) тесла (Тл) кулон (Кл) |
сантиметр (см) грамм (г) секунда (с) дина (дин) эрг (эрг) бар (бар) гаусс (Гс) франклин (Фр) |
При решении любой физической (математической) задачи надо очень внимательно подходить к используемым единицам измерения. Ни в коем случае их нельзя "смешивать" при решении одной задачи. Если вы начали решать задачу в системе СИ, то надо ее придерживаться до конца решения задачи. В противном случае вместо правильного ответа вы получите "винегрет" из разных величин.
Но, как же быть, если в условии задачи присутствуют данные, выраженные через различные системы измерения? Ответ прост и очевиден: надо все данные привести к одной системе измерения! Ниже представлены преобразования единиц различных систем измерения.
| 1 метр = 102 см | 1 джоуль = 107 эрг | 1 дюйм = 2,54 см | 1 атомная ед.м. = 1,6605·10-27 кг |
| 1 километр = 105 см | 1 паскаль = 10-5 бар | 1 м = 39,37 дюйма | 1 кВт·час = 3,6·106 Дж |
| 1 килограмм = 103 г | 1 тесла = 104 Гс | 1 миля = 1,609 км | 1 электронвольт = 1,602·10-19 Дж |
| 1 ньютон = 105 дин | 1 кулон = 2,9979·109 Фр | 1 ангстрем = 10-10 м | 1 лош.сила = 745,7 Вт |
2. Экспоненциальное представление чисел
Мир настолько многообразен, что, используемые для его описания, единицы измерения, могут иметь очень большие или очень малые значения. Пользоваться обычной записью таких значений очень неудобно, поскольку они очень громоздки. Поэтому, для более удобной работы с очень большими или очень малыми величинами используют экспоненциальное представление чисел. В этом представлении нули выражаются в степенях числа 10. Чтобы определить степень, нужно подсчитать все цифры справа налево до первой цифры.
|
Например:
Расстояние от Земли до Луны составляет примерно 384400000 метров = 3,844·108 м |
Для очень малых величин степень числа 10 имеет отрицательный знак. В этом случае надо подсчитать кол-во цифр слева направо от десятичной запятой до места после первой ненулевой цифры.
|
Например:
Диаметр молекулы воды составляет 0,00000000028 метров = 2,8·10-10 м |
Если число больше 10, то в экспоненциальном представлении оно будет иметь положительную степень, если меньше 1 - отрицательную.
3. Точность измерений
Одним из важных факторов успешного решения задачи является точность измерений (не путать с точностью вычислений).
| 16 августа 2009 года в Берлине на ЧМ по легкой атлетике легендарный Усейн Болт установил феноменальный рекорд в беге на 100 метров - 9,58 секунды. |
Из этого сообщения мы имеем два измерения (расстояние и время), в каждом из которых по три значащих цифры.
| Значащими цифрами считаются те, которые были фактически получены в ходе измерения. |
Чтобы определить среднюю скорость мирового рекорда, надо разделить путь на время. Получим 10,4384133611 м/с. Казалось бы, мы получили очень точный результат средней скорости атлета. Однако, это не совсем так, а вернее, совсем не так. Поскольку после измерения расстояния и времени были получены по три значащие цифры, то точность измерений не может возрасти до пяти-семи-десяти… значащих цифр. Ведь нельзя же при помощи простой миллиметровой линейки получить результат измерения до микрон!
В нашем примере следует ограничиться тремя значащими цифрами, т.е., средняя скорость У.Болта будет равна 10,4 м/с.
Здесь следует упомянуть еще об одном существенном нюансе вычислений - округлении числа.
| Правило округления очень простое: если цифра справа от округляемой равна или больше 5, то округление выполняется в сторону увеличения; в противном случае - в сторону уменьшения. Например: 1,92=1,9; 2,47=2,5; 39,6=40 |
А что изменится, если сказать, что У.Болт пробежал 100,00 м за 9,58 с ? Вроде бы, ничего не изменилось. Но! В измерении расстояния теперь указано пять значащих цифр! Как теперь (до какой точности) правильно вычислить среднюю скорость спортсмена? В этом случае надо придерживаться следующих правил определения чисел с разным кол-вом значащих цифр.
- При умножении или делении чисел результат будет иметь то же кол-во значащих цифр, что и исходное число с наименьшим кол-вом значащих цифр.
- При сложении или вычитании чисел нужно расположить их в столбик и выровнять по положению десятичной запятой - самая последняя значащая цифра в результате будет соответствовать самой правой значащей цифре в том столбце, в котором все числа в столбике имеют значащие цифры.
Например:

Округляем до 8,4
4. Немного алгебры и тригонометрии
В физике, как и в любой точной науке, используется очень много уравнений. Чтобы правильно производить вычисления надо свободно пользоваться приемами манипулирования частями уравнения. Правила очень просты и их несложно запомнить:
Левую и правую части равенства можно менять местами: (Z=XY) ≡ (XY=Z)
Левую и правую части равенства можно делить на одно и то же число, умножать на одно и то же число, прибавлять одно и то же число, вычитать одно и то же число, возводить в одну и ту же степень:
(Y=2X) ≡ (Y/2=X) ≡ (1/2=X/Y)
(Y=2+X) ≡ (Y-X=2) ≡ (X=Y-2)
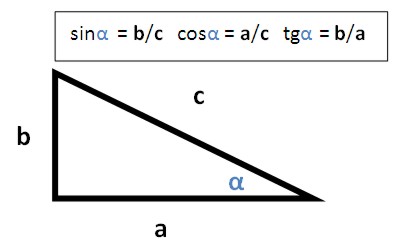
И, "на закуску" - синус, косинус, тангенс.