Физика - это просто!

МЕХАНИКА

· Измерения. Системы измерений
· Перемещение
· Скорость
· Ускорение
· Нестандартные связи
· Векторы
· S, V, a - векторные величины
· Первый закон Ньютона
· Второй закон Ньютона
· Третий закон Ньютона
· Гравитация
· Трение
· Свободное падение
· Вращательное движение
· Закон всемирного тяготения
· Работа
· Энергия
· Импульс
· Закон сохранения импульса
· Измерение скорости с помощью ЗСИ
· Параметры вращательного движения
· Вращательное движение и векторы
· Момент силы
· Условие равновесного состояния
· Вращательное движение и 2 закон Ньютона
· Момент инерции протяженного объекта
· Энергия и работа при вращательном движении
· Момент импульса
· Закон Гука
· Простое гармоническое движение
· Энергия гармонического движения
· Маятниковое движение

ТЕРМОДИНАМИКА

ЭЛЕКТРОМАГНЕТИЗМ

ФИЗИКА-ВУЗ

Гравитация

1. Движение по наклонной плоскости

На поверхности Земли сила тяжести (гравитация) постоянна и равна произведению массы падающего тела на ускорение свободного падения: F_g = mg

Следует заметить, что ускорение свободного падения величина постоянная: g=9,8 м/с², и направлена к центру Земли. Исходя из этого можно сказать, что тела с разной массой будут падать на Землю одинаково быстро. Как же так? Если бросить с одинаковой высоты кусочек ваты и кирпич, то последний проделает свой путь до земли быстрее. Не забывайте о сопротивлении воздуха! Для ваты оно будет существенным, поскольку ее плотность очень мала. В безвоздушном пространстве кирпич и вата упадут одновременно.

1. Движение по наклонной плоскости

Шар движется по наклонной плоскости длиной 10 метров, угол наклона плоскости 30°. Какова будет скорость шара в конце плоскости?

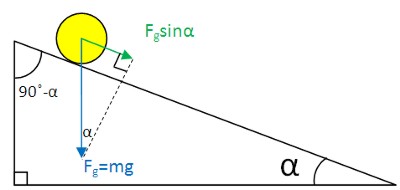
На шар действует только сила тяжести F_g, направленная вниз перпендикулярно к основанию плоскости. Под действием этой силы (составляющей, направленной вдоль поверхности плоскости) шар будет двигаться. Чему будет равна составляющая силы тяжести, действующей вдоль наклонной плоскости?

Для определения составляющей необходимо знать угол между вектором силы F_g и наклонной плоскостью.

Определить угол довольно просто:

• сумма углов любого треугольника равна 180°;
• угол между вектором силы F_g и основанием наклонной плоскости равен 90°;
• угол между наклонной плоскостью и ее основанием равен α

Исходя из вышесказанного, искомый угол будет равен: 180° - 90° - α = 90° - α

Из тригонометрии:

F_gнакл = F_g·cos(90°-α)

sinα = cos(90°-α)

F_gнакл = F_g·sinα

Это действительно так:

• при α=90° (вертикальная плоскость) F_gнакл = F_g
• при α=0° (горизонтальная плоскость) F_gнакл = 0

Определим ускорение шара из известной формулы:

F_g·sinα = m·a

a = F_g·sinα/m

F_g = m·g

a = m·g·sinα/m = g·sinα

Ускорение шара вдоль наклонной плоскости не зависит от массы шара, а только от угла наклона плоскости.

Определяем скорость шара в конце плоскости:

V₁² - V₀² = 2·a·s

(V₀=0) - шар начинает движение с места

V₁² = √2·a·s

V = 2·g·sinα·S = √2·9,8·0,5·10 = √98 = 10 м/с

Обратите внимание на формулу! Скорость тела в конце наклонной плоскости будет зависеть только от угла наклона плоскости и ее длины.

В нашем случае скорость 10 м/с в конце плоскости будет иметь и бильярдный шар, и легковой автомобиль, и самосвал, и школьник на санках. Конечно же, трение мы не учитываем.