Способы задания функции
Математическая функция может задаваться тремя способами:
- формулой;
- таблицей;
- графиком.
Функция может быть задана формулой, например:
y = 2x y = x2+10 y = lg(x) y = sin(x)
Давая некие значения независимой переменной (аргументу) x, при помощи формулы вычисляют соответствующие значения зависимой переменной y.
Например, при x=1 в вышеприведенных функциях переменная y примет следующие значения:
y = 2·1 = 2 y = 12+10 = 11 y = lg(1) = 0 y = sin(1) = 57°
Следует обратить внимание, что при задании функции формулой, не всегда аргумент может принимать любые значения. Например, в функции, заданной формулой y = lg(x), аргумент может принимать только положительные значения.
При табличном задании функции любому значению аргумента, имеющегося в таблице, соответствует только одно значение функции. Например:
| x | y |
|---|---|
| 0 | 1 |
| -2 | 10 |
| 5 | 14 |
| 25 | 11 |
| -7 | 9 |
| 33 | 200 |
При графическом задании функции берется по оси абсцисс нужное значение аргумента, после чего проводится вертикальная линия до пересечения с графиком функции, из этой точки проводится горизонтальная линия до пересечения с осью ординат, где будет отображено значение зависимой переменной y.
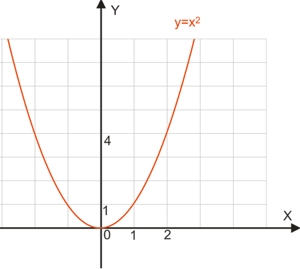
Задание функции графиком очень наглядно, но, как правило, позволяет найти только приближенное значение функции.
На рисунке выше приведен график квадратичной функции y=x2.
Для аргумента x=1 будет соответствовать значение функции y=1; для x=2; y=4. Точно такие же значения функции будут получены для аргументов x=-1; x=-2.
