График функции
Для любой функции может быть построен ее график.
Плоскость, в которой построена прямоугольная система координат, называется координатной плоскостью.
Любая точка координатной плоскости имеет свои координаты - некое значение абсциссы (координата x), и ординаты (координата y).
Некое выеделенное каким-либо образом множество точек на координатной плоскости называют графиком.

На рисунке показан график, состоящий из 5 точек, имеющих следующие координаты (x, y):
- A (2;3);
- B (4;1);
- C (1;-2);
- D (-1;-3);
- F (-3;3).
График может состоять из конечного числа точек, но, чаще график включает бесконечное множество точек в виде линии.
Некая линия будет являться графиком функции F=y(x) в случае, если каждому значению аргумента x будет соответствовать единственное значение зависимой переменной y.
Ранее уже было сказано о трех способах задания функций: формулой, таблицей, собственно графиком.
Чаще всего функция задается при помощи формулы, в которой ординаты точек графика функции находятся после подстановки в формулу соответствующих абсцисс этих точек.
Рассмотрим график некой абстрактной функции F=y(x), показанной на рисунке ниже.

График функции F=±a + y(x) получится путем сдвига графика исходной функции (красный цвет) вдоль оси ординат вверх (при положительном а - зеленый цвет) или вниз (при отрицательном а - синий цвет).
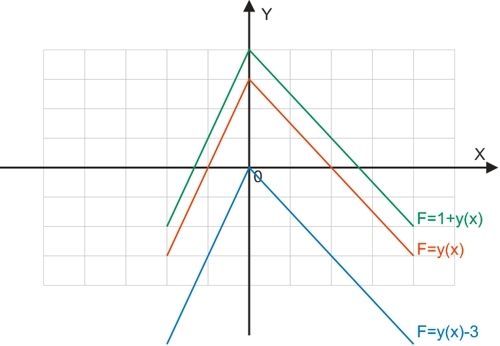
График функции F=y(x±b) получится путем сдвига графика исходной функции (красный цвет) вдоль оси абсцисс влево (при положительном b - синий цвет) или вправо (при отрицательном b - зеленый цвет).
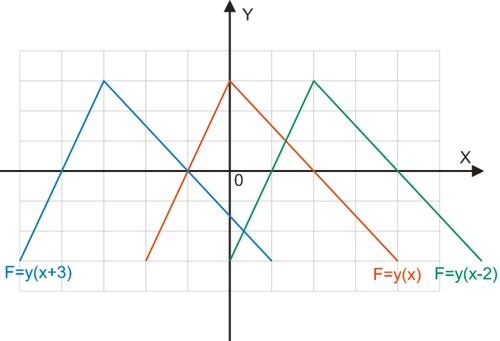
График функции F=m·y(x) получится путем сжатия (0<m<1 - зеленый цвет - точки графика как бы сближаются с осью абсцисс) или растяжения (m>1 - синий цвет - точки графика как бы удаляются от оси абсцисс) графика исходной функции (красный цвет) от оси абсцисс вдоль оси ординат в m раз.
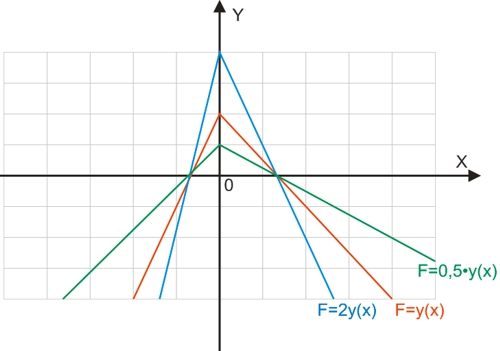
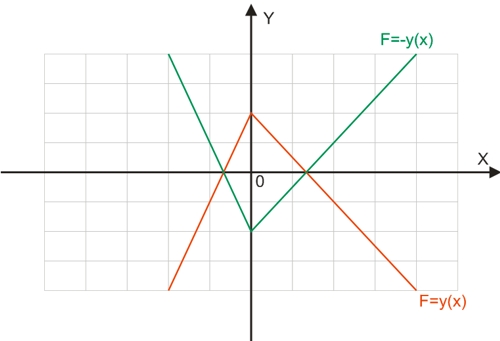
График функции F=-y(x) является зеркальным отображением исходного графика (красный цвет) относительно оси абсцисс.