Функции вида y=sin(x), y=cos(x)
График функции вида y=sin(x) называется синусоидой; график вида y=cos(x) - косинусоидой.
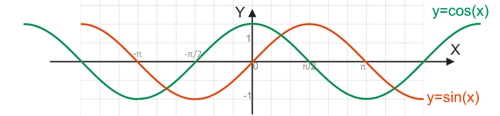
Свойства синусоиды и косинусоиды:
- Область определения синусоиды и косинусоиды - область всех действительных чисел;
- Функции y=sin(x), y=cos(x) являются периодическими с периодом 2π. На этом промежутке максимальное значение, которое могут принимать обе функции, равно 1; минимальное = -1. Это дает возможность рассматривать любой промежуток функций длиной в 2π, при этом другие промежутки будут получаться из рассматриваемого путем прибавления к нему целого числа удвоенных периодов;
- Функция y=sin(x) является возрастающей на всех промежутках, удовлетворяющих неравенству:
(-π/2 + 2kπ) ≤ x ≤ (π/2 + 2kπ)
и убывающей на всех промежутках, удовлетворяющих неравенству:
(π/2 + 2kπ) ≤ x ≤ (3π/2 + 2kπ)
(k - целое число). См. рисунок выше (красный график). - Функция y=cos(x) является возрастающей на всех промежутках, удовлетворяющих неравенству:
(-π + 2kπ) ≤ x ≤ (2kπ)
и убывающей на всех промежутках, удовлетворяющих неравенству:
(2kπ) ≤ x ≤ (π + 2kπ)
(k - целое число). См. рисунок выше (зеленый график). - Корни функции y=sin(x): все точки, удовлетворяющие равенству x=kπ
- Корни функции y=cos(x): все точки, удовлетворяющие равенству x=π/2 + kπ
- Функция y=sin(x) является нечетной, т. к. sin(-x)=-sin(x) ее график симметричен относительно оси ординат;
- Функция y=cos(x) является четной, т. к. cos(-x)=cos(x) ее график симметричен относительно начала координат.
Для построения синусоиды достаточно построить график функции на отрезке от 0 до π/2. Остальные части полного периода синусоиды будут копией построенного графика:
- на участке от -π/2 до 0 - это будет линия, симметричная относительно начала координат линии, построенной на промежутке от 0 до π/2;
- поскольку sin(π/2-x)=sin(π/2+x), построенный отрезок синусоиды на промежутке от -π/2 до +π/2 будет симметричен относительно оси x=π/2, графику на промежутке от π/2 до 3π/2;
- поскольку cos(x)=sin(π/2+x), то косинусоида может быть построена путем копирования и смещения синусоиды на промежуток (-π/2).
Функции вида y=tg(x), y=ctg(x)
График функции вида y=tg(x) называется тангенсоидой; график вида y=ctg(x) - котангенсоидой.
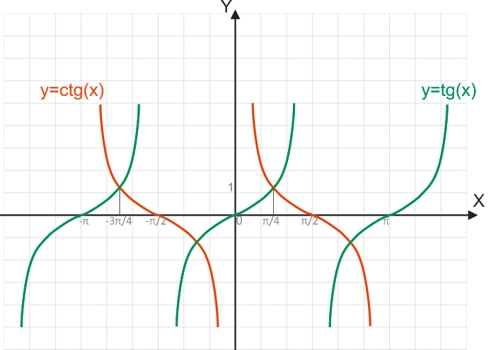
Свойства тангенсоиды и котангенсоиды:
- Область определения тангенсоиды - область всех действительных чисел за исключением точек, обращающих функцию cos(x) в ноль, т. е., удовлетворяющих условию x=(π/2+kπ) (k - целое число);
- Область определения котангенсоиды - область всех действительных чисел за исключением точек, обращающих функцию sin(x) в ноль, т. е., удовлетворяющих условию x=kπ (k - целое число);
- Функции y=tg(x), y=ctg(x) являются периодическими с периодом π. Это дает возможность рассматривать любой промежуток функций длиной в π, при этом другие промежутки будут получаться из рассматриваемого путем прибавления к нему целого числа периодов;
- Функция y=tg(x) является возрастающей, как правило, данная функция рассматривается на промежутке от -π/2 до +π/2;
- Функция y=ctg(x) является убывающей, как правило, данная функция рассматривается на промежутке от 0 до +π;
- Корни функции y=tg(x): все точки, удовлетворяющие равенству x=kπ
- Корни функции y=ctg(x): все точки, удовлетворяющие равенству x=π/2 + kπ
- Функция y=tg(x) является нечетной, т. к. tg(-x)=-tg(x) ее график симметричен относительно оси ординат;
- Функция y=ctg(x) является нечетной, т. к. ctg(-x)=-ctg(x) ее график симметричен относительно оси ординат.
Поскольку, ctg(x)=tg(π2-x)=-tg(x-π/2), то котангенсоида может быть получена копированием и переносом тангенсоиды на +π/2, при этом соответствующие значения ординаты заменяются на противоположные. Говоря проще, котангенсоида является зеркальным отображением тангенсоиды относительно вертикальной оси с последующим смещением вправо на π/2.
