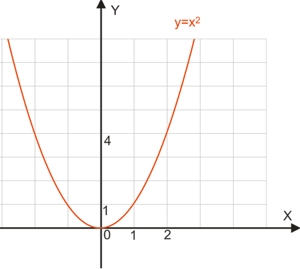
Функция y=x2
График функции y=x2 называется параболой.
Свойства функции y=x2:
- Область определения функции y=x2 - область всех действительных чисел;
- Функция y=x2 на интервале (-∞; 0) является убывающей и возрастающей на интервале (0; ∞);
- График функции y=x2 проходит через начало координат;
- Функция y=x2 является четной, ее график симметричен относительно оси ординат;
- Функция y=x2 не является периодической функцией.
Все точки параболы y=x2 лежат выше оси абсцисс, лишь только ее вершина касается оси абсциссс в точке с координатами (0; 0).
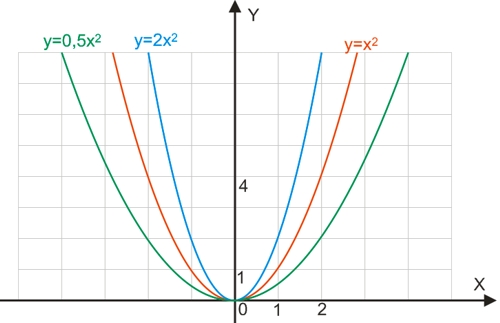
Функция y=ax2
График функции y=ax2 также является параболой, ветви которой, в зависимости от значения коэффициента a, растягиваются или сжимаются:
- при |a|>1 парабола y=x2 растягивается от оси абсцисс вдоль оси ординат, при этом величина растяжения составляет a раз;
- при 0<|a|<1 парабола y=x2 сжимается к оси абсцисс вдоль оси ординат, при этом величина сжатия составляет 1/a раз;
Свойства функции y=ax2:
- Область определения функции y=ax2 - область всех действительных чисел;
- Функция y=ax2:
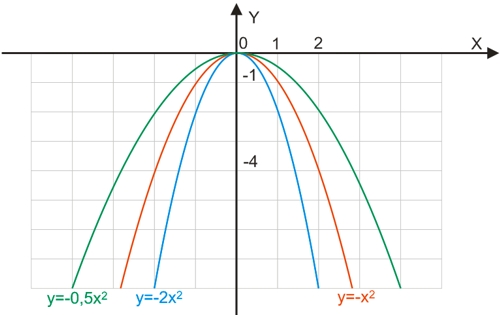
- при a>0 на интервале (-∞; 0) является убывающей и возрастающей на интервале (0; ∞) - ветви параболы направлены вверх;
- при a<0 на интервале (-∞; 0) является возрастающей и убывающей на интервале (0; ∞) - ветви параболы направлены вниз;
- График функции y=ax2 проходит через начало координат;
- Функция y=ax2 является четной, ее график симметричен относительно оси ординат;
- Функция y=ax2 не является периодической функцией.
Квадратичная функция y=ax2+bx+c
Квадратичной называется функция вида y=ax2+bx+c, где a, b, c - заданные действительные числа, при этом: a≠0.
Рассмотренные выше функции y=x2 и y=ax2 являются частным случаем квадратичной функции:
y=x2; a=1, b=0, c=0 y=ax2; b=0, c=0
График квадратичной функции y=ax2+bx+c получается из графика функции y=ax2, путем его параллельного переноса вверх-вниз и влево-вправо относительно начала координат - направление и величина смещения графика зависит от коэффициентов b и c.
Главной задачей при построении графика квадратичной функции является нахождение координат вершины параболы (x0; y0). После того, как координаты вершины параболы найдены, уже нет никаких проблем построить график функции y=ax2.
Для быстрого и удобного нахождения координат вершины параболы, являющейся графиком квадратичной функции вида y=ax2+bx+c, умные люди применили метод выделения полного квадрата, благодаря чему, квадратичная функция была приведена к виду:
y=a(x-x0)2 + y0
Выделение полного квадрата квадратичной функции:
y=ax2+bx+c= a(x2+x·b/a+c/a)= a(x2+2x·b/(2a)+(b/(2a))2-(b/(2a))2+c/a)= a((x+b/(2a))2-(b/(2a))2+c/a)= a((x+b/(2a))2-(b2/(4a2)-c/a))= a((x+b/(2a))2-(b2-4ac)/(4a2))= a(x+b/(2a))2-(b2-4ac)/4a= a(x-(-b)/(2a))2+(-(b2-4ac))/4a
Таким образом, квадратичная функция y=ax2+bx+c трансформировалась в функцию вида y=a(x-x0)2+y0, где:
x0 = -b/(2a) y0 = -(b2-4ac)/4a
Точка с координатами (x0; y0) является вершиной параболы y=ax2+bx+c.
При a>0 ветви параболы направлены вверх и квадратичная функция в точке (x0; y0) будет принимать минимум, при a<0 ветви параболы направлены вниз и в точке (x0; y0) квадратичная функция будет принимать максимум.
В формуле исходной квадратичной функции коэффициент b влияет на смещение графика функции, как вдоль оси абсцисс, так и вдоль оси ординат; коэффициент с - смещает график только вдоль оси ординат.
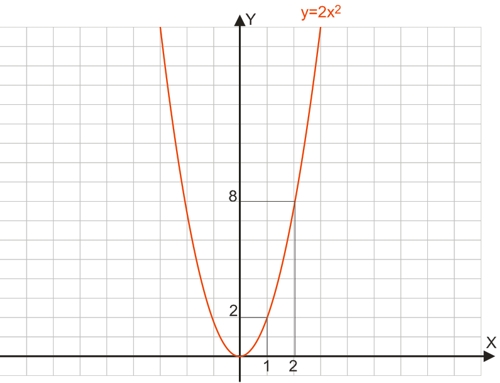
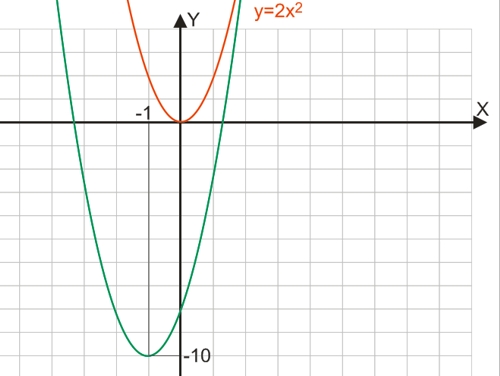
В качестве примера построим график квадратичной функции y=2x2+4x-8.
График данной функции будет получен путем переноса вершины параболы y=2x2.
Наша задача - найти координаты вершины функции y=2x2+4x-8.
Это сделать достаточно просто, используя вышеприведенный метод выделения полного квадрата квадратичной функции.
x0 = -b/(2a) x0 = -4/(2·2) = -1 y0 = -(b2-4ac)/4a y0 = -(42-4·2·(-8))/4·2 = -10
Все, что нам остается сделать - провести параллельный перенос графика из начала координат в точку с координатами (-1; -10):
Для того, чтобы узнать в каких точках график пересекает ось абсцисс, надо решить квадратное уравнение:
2x2+4x-8 = 0 x1,2 = (-4±√(16+64))/4 x1,2 = -1±√5 x1 ≈ -3,24 x2 ≈ 1,24
