Обратимые и обратные функции
Обратимой называется функция в которой произвольному значению функции соответствует единственное значение аргумента.
Примеры обратимых функций:
y=2x+5 y=x3 y=2/x
Поскольку в обратимой функции любому значению y соответствует единственное значение x, то y обратимой функции может выполнять роль аргумента (независимой переменной), а x - роль функции (зависимой переменной). Говоря, проще, в обратимых функциях y и x могут как бы меняться местами.
Исходная обратимая функция и функция, полученная из нее путем замены x на y и y на x, называются обратными.
Примеры обратных функций:
y=2x+5; x=2y+5; y=(x-5)/2 y=x3; x=y3; y=x1/3 y=2/x; x=2/y; y=2/x
Если взять функцию y=x2, то она не является обратной, поскольку значение функции имеет несколько значений аргумента, например y=4, при x=2; x=-2.
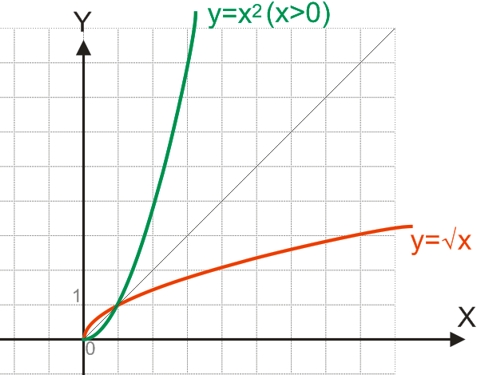
Однако, если рассматривать данную функцию только на множестве положительных чисел, она будет обратимой:
y=x2; x=y2; y=x1/2=√x
Графики функций будут симметричны относительно прямой y=x:
Функция y=arcsin(x)
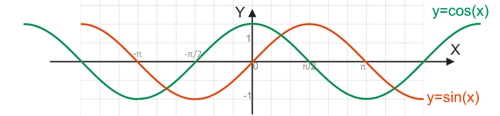
Поскольку функция y=sin(x) является периодической, она не является обратимой.
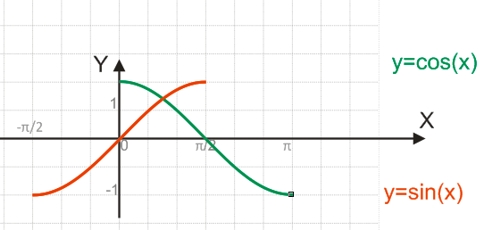
Для построения функции, обратимой y=sin(x), необходимо взять один из полупериодов функции, обычно это отрезок [-π/2;π/2], на котором функция обратима.
y=sin(x) x=sin(y); y=arcsin(x)
График функции y=arcsin(x):
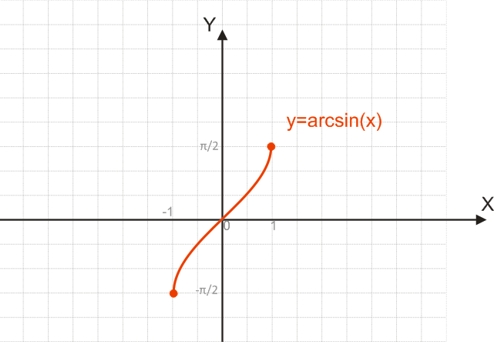
Например, чтобы найти arcsin(1), можно воспользоваться равенством 1=sin(y). Угол на отрезке [-π/2;π/2], синус которого равняется 1, будет равен 90° или π/2.
Функция y=arccos(x)
Поскольку функция y=cos(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=cos(x), необходимо взять один из полупериодов функции, обычно это отрезок [0;π], на котором функция обратима.
y=cos(x) x=cos(y); y=arccos(x)
График функции y=arccos(x):
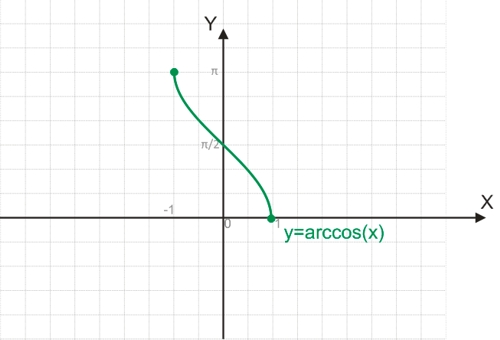
Например, чтобы найти arccos(1), можно воспользоваться равенством 1=cos(y). Угол на отрезке [0;π], косинус которого равняется 1, будет равен 0.
Функция y=arctg(x)
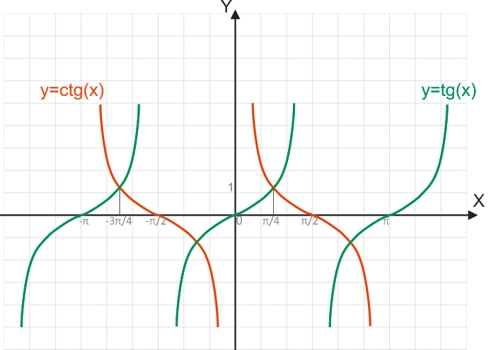
Поскольку функция y=tg(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=tg(x), необходимо рассматривать тангенсоиду на отрезке [-π/2;π/2], на котором функция обратима.
y=tg(x) x=tg(y); y=arctg(x)
График функции y=arctg(x):
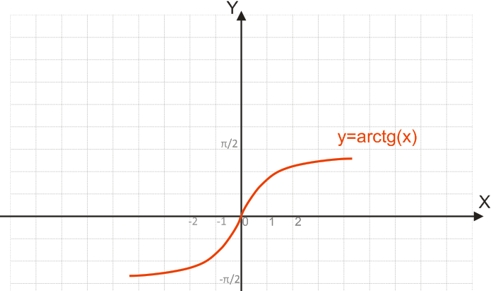
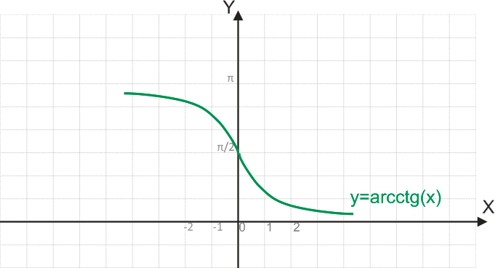
Функция y=arcctg(x)
Поскольку функция y=ctg(x) является периодической, она не является обратимой.
Для построения функции, обратимой y=ctg(x), необходимо рассматривать котангенсоиду на отрезке [0;π], на котором функция обратима.
y=ctg(x) x=ctg(y); y=arcctg(x)
График функции y=arcctg(x):