ФИЗИКА - ЭТО ПРОСТО!

Что изучает физика?

1. Измерения. Системы измерений
2. Перемещение
3. Скорость
4. Ускорение
5. Нестандартные связи
6. Векторы
7. S, V, a - векторные величины
8. Первый закон Ньютона
9. Второй закон Ньютона
10. Третий закон Ньютона
11. Гравитация
12. Трение
13. Свободное падение
14. Вращательное движение
15. Закон всемирного тяготения
16. Работа
17. Энергия

Третий закон Ньютона Учитываем трение Состояние равновесия Сила действия одного объекта на другой равна по величине силе противодействия другого объекта, направленной в противоположную сторону.

1. Учитываем трение

Многие из вас видели как силачи, устанавливая рекорды, тянут за собой большегрузные автомобили или даже самолеты. В этом случае результирующая сила равна:

ΣF = F_канат - F_трение

Когда сила, приложенная силачом к канату, больше силы трения, то грузовик начинает ускоренное движение:

ΣF = F_канат - F_трение = ma

Одна часть силача расходуется на преодоление силы трения, другая - на ускорение:

F_канат = F_трение + ma

Как видим из формулы, атлету тем тяжелее, чем выше сила трения и больше масса объекта. Действительно, тянуть санки по снегу гораздо легче, чем толкать автомобиль, застрявший в грязи.

---

2. Состояние равновесия

Считается, что объект находится в состоянии равновесия, если его ускорение равно нулю, т.е. действующая сила равна нулю.

На объект могут действовать разнообразные силы, но в состоянии равновесия их векторная сумма равна нулю.

Рассмотрим случай с фонарем, освещающим вход в помещение:



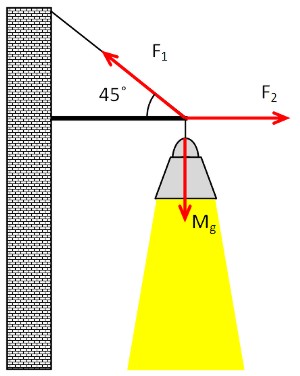
Пусть вес фонаря равен 10 Н. Какой должна быть прочность проволоки (сила F₁), чтобы удержать этот фонарь? Угол крепления проволоки к фонарю равен 45°.

Решение задачи.

Поскольку фонарь не должен упасть, то действующая на него, результирующая сила должна быть равна нулю.

Вес фонаря (M_g) должен быть уравновешен силой натяжения проволоки F₁.

В нашем случае единственной силой, которая может удержать фонарь от падения, является составляющая силы F₁.

Сила сопротивления горизонтальной балки F₂ направлена только по горизонтали и не оказывает никакого влияния на вертикальную составляющую.

Определяем Y-составляющую силы F₁:

F_1y = F₁·sin45° = M_g

Натяжение проволоки:

F₁ = F_1y/sin45° = M_g/sin45° = 10/(0,7) = 14 Н

Т.о., в нашем случае, чтобы проволока не порвалась, она должна выдерживать силу примерно равную 14 Н.

Попробуйте самостоятельно решить другую задачу:

Какую прочность в нашем случае должна иметь балка, чтобы выдержать силу сопротивления F₂ (F₁=14 Н)?

Решение задачи смотрите на странице ответов.