Закон всемирного тяготения
Сэр Исаак Ньютон, получив по голове яблоком, вывел закон всемирного тяготения, который гласит:
Любые два тела притягиваются друг к другу с силой прямо пропорциональной произведению масс тела и обратно пропорциональной квадрату расстояния между ними:
F = (Gm1m2)/R2, где
m1, m2 - массы тел
R - расстояние между центрами тел
G = 6,67·10-11 Нм2/кг - константа
Определим ускорение свободного падения на поверхности Земли:
Fg = mтелаg = (GmтелаmЗемли)/R2
R (радиус Земли) = 6,38·106 м
mЗемли = 5,97·1024 кг
mтелаg = (GmтелаmЗемли)/R2 или g = (GmЗемли)/R2
Обратите внимание, что ускорение свободного падения не зависит от массы тела!
g = 6,67·10-11·5,97·1024/(6,38·106) = 398,2/40,7 = 9,8 м/с2
Мы говорили ранее, что силу тяжести (гравитационное притяжение) называют весом.
На поверхности Земли вес и масса тела имеют одинаковое значение. Но по мере удаления от Земли вес тела будет уменьшаться (т.к. будет увеличиваться расстояние между центром Земли и телом), а масса будет оставаться постоянной (поскольку масса - это выражение инерции тела). Масса измеряется в килограммах, вес - в ньютонах.
Благодаря силе гравитации, небесные тела вращаются друг относительно друга: Луна вокруг Земли; Земля вокруг Солнца; Солнце вокруг центра нашей Галактики и т.д. При этом тела удерживаются центробежной силой, которую обеспечивает сила гравитации.
Это же относится и к искусственным телам (спутникам), вращающимся вокруг Земли. Окружность по которой спутник вращается, называется орбитой вращения.При этом на спутник действует центробежная сила:
Fц = (mспутникаV2)/R
Сила гравитации:
Fg = (GmспутникаmЗемли)/R2
Fц = Fg = (mспутникаV2)/R = (GmспутникаmЗемли)/R2
V2 = (GmЗемли)/R; V = √(GmЗемли)/R
По этой формуле можно вычислить скорость любого тела, вращающегося по орбите с радиусом R вокруг Земли.
Естественным спутником Земли является Луна. Определим ее линейную скорость на орбите:
Масса Земли = 5,97·1024 кг
R - это расстояние между центром Земли и центром Луны. Чтобы определить это расстояние, нам надо сложить три величины: радиус Земли; радиус Луны; расстояние от Земли до Луны.
Rлуны = 1738 км = 1,74·106 м
Rземли = 6371 км = 6,37·106 м
Rзл = 384400 км = 384,4·106 м
Общее расстояние между центрами планет: R = 392,5·106 м
Линейная скорость Луны:
V = √(GmЗемли)/R = √6,67·10-11·5,98·1024/392,5·106 = 1000 м/с = 3600 км/ч
Луна движется по круговой орбите вокруг Земли с линейной скоростью в 3600 км/ч!
Определим теперь период обращения Луны вокруг Земли. За период обращения Луна преодолевает расстояние, равное длине орбиты - 2πR. Орбитальная скорость Луны: V = 2πR/T; с другой стороны: V = √(GmЗемли)/R:
2πR/T = √(GmЗемли)/R отсюда T = 2π√R3/GmЗемли
T = 6,28·√(60,7·1024)/6,67·10-11·5,98·1024 = 3,9·105 с
Период обращения Луны вокруг Земли составляет 2 449 200 секунд, или 40 820 минут, или 680 часов, или 28,3 суток.
1. Вертикальное вращение
Ранее в цирках был очень популярным трюк в котором велосипедист (мотоциклист) делал полный оборот внутри окружности, расположенной вертикально.
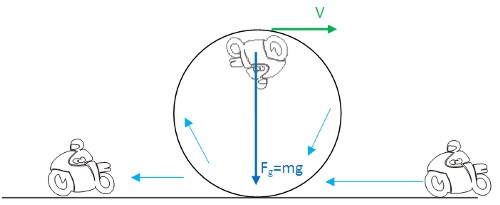
Какой же минимальной скоростью должен обладать трюкач, чтобы в верхней точке не свалиться вниз?
Для прохождения верхней точки без падения тело должно обладать скоростью, создающей такую центробежную силу, которая бы компенсировала силу тяжести.
Центробежная сила: Fц = mV2/R
Сила тяжести: Fg = mg
Fц = Fg; mV2/R = mg; V = √Rg
И опять обратите внимание, что в расчетах отсутствует масса тела! Следует учесть, что это скорость, которой должно обладать тело в верхней точке!
Допустим, что на арене цирка установлена окружность с радиусом 10 метров. Рассчитаем безопасную скорость для трюка:
V = √Rg = √10·9,8 = 10 м/с = 36 км/ч
