Вращательное движение
Ранее рассматривались характеристики прямолинейного движения: перемещение, скорость, ускорение. Их аналогами при вращательном движении являются: угловое перемещение, угловая скорость, угловое ускорение.
- Роль перемещения во вращательном движении играет угол;
- Величина угла поворота за единицу времени - это угловая скорость;
- Изменение угловой скорости за единицу времени - это угловое ускорение.
1. Равномерное вращательное движение
Во время равномерного вращательного движения тело совершает движение по окружности с одинаковой скоростью, но с изменяющимся направлением. Например, такое движение совершают стрелки часов по циферблату.
Допустим, шар равномерно вращается на нити длиной 1 метр. При этом он будет описывать окружность с радиусом 1 метр. Длина такой окружности: C = 2πR = 6,28 м
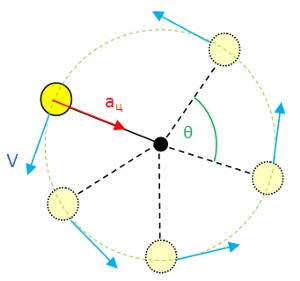
Время, за которое шар полностью делает один полный оборот по окружности, называется периодом вращения - T.
Чтобы вычислить линейную скорость шара, необходимо разделить перемещение на время, т.е. длину окружности на период вращения:
V = C/T = 2πR/T
Период вращения:
T = 2πR/V
Если наш шар будет делать один оборот за 1 секунду (период вращения = 1с), то его линейная скорость:
V = 6,28/1 = 6,28 м/с
2. Центробежное ускорение
В любой точке вращательного движения шара вектор его линейной скорости направлен перпендикулярно радиусу. Нетрудно догадаться, что при таком вращении по окружности, вектор линейной скорости шара постоянно меняет свое направление. Ускорение, характеризующее такое изменение скорости, называется центробежным (центростремительным) ускорением.
| Составляющая вектора скорости, перпендикулярная радиусу вращения, является касательной к траектории движения и называется тангенциальной составляющей. Перпендикулярная ей компонента называется нормальной составляющей |
Во время равномерного вращательного движения меняется только направление вектора скорости, но не величина! Поэтому линейное ускорение = 0. Изменение линейной скорости поддерживается центробежным ускорением, которое направлено к центру окружности вращения перпендикулярно вектору скорости - aц.
Центробежное ускорение можно вычислить по формуле: aц = V2/R
Чем больше линейная скорость тела и меньше радиус вращения, тем центробежное ускорение больше.
3. Центробежная сила
Из прямолинейного движения мы знаем, что сила равна произведению массы тела на его ускорение.
При равномерном вращательном движении на вращающееся тело действует центробежная сила:
Fц = maц = mV2/R
Если наш шарик весит 1 кг, то для удержания его на окружности понадобится центробежная сила:
Fц = 1·6,282/1 = 39,4 Н
С центробежной силой мы сталкиваемся в повседневной жизни при любом повороте.
Задача №1: расчитать, какую максимальную скорость может развить тело в повороте с радиусом 30 метров при коэффициенте трения 0,9, чтобы "вписаться" в этот поворот.
Сила трения должна уравновесить центробежную силу:
Fц = mV2/R; Fтр = μmg
Fц = Fтр; mV2/R = μmg
V = √μmgR/m = √μgR = √0,9·9,8·30 = 16,3 м/с = 58,5 км/ч
Ответ: 58,5 км/ч
Обратите внимание, что скорость в повороте не зависит от массы тела!
Наверняка вы обращали внимание, что некоторые повороты на шоссе имеют некоторый наклон внутрь поворота. Такие повороты "легче" проходить, вернее, можно проходить с бОльшей скоростью. Рассмотрим какие силы действуют на автомобиль в таком повороте с наклоном. При этом силу трения учитывать не будем, а центробежное ускорение будет компенсироваться только горизонтальной составляющей силы тяжести:
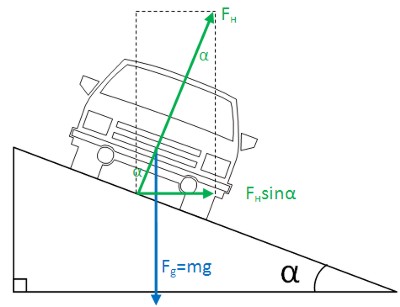
Fц = mV2/R или Fц = Fнsinα
В вертикальном направлении на тело действует сила тяжести Fg = mg, которая уравновешивается вертикальной составляющей нормальной силы Fнcosα:
Fнcosα = mg, отсюда: Fн = mg/cosα
Подставляем значение нормальной силы в исходную формулу:
Fц = Fнsinα = (mg/cosα)sinα = mg·sinα/cosα = mg·tgα
Т.о., угол наклона дорожного полотна:
α = arctg(Fц/mg) = arctg(mV2/mgR) = arctg(V2/gR)
Опять обратите внимание, что в расчетах не участвует масса тела!
Задача №2: на некотором участке шоссе имеется поворот с радиусом 100 метров. Средняя скорость прохождения этого участка дороги автомобилями 108 км/ч (30 м/с). Каким должен быть безопасный угол наклона полотна дороги на этом участке, чтобы автомобиль "не вылетел" (трением пренебречь)?
α = arctg(V2/gR) = arctg(302/9,8·100) = 0,91 = 42°
Ответ: 42°. Довольно приличный угол. Но, не забывайте, что в наших расчетах мы не принимаем во внимание силу трения дорожного полотна.4. Градусы и радианы
Многие путаются в понимании угловых величин.
При вращательном движении основной единицей измерения углового перемещения является радиан.
- 2π радиан = 360° - полная окружность
- π радиан = 180° - половина окружности
- π/2 радиан = 90° - четверть окружности
Чтобы перевести градусы в радианы, необходимо значение угла разделить на 360° и умножить на 2π. Например:
- 45° = (45°/360°)·2π = π/4 радиан
- 30° = (30°/360°)·2π = π/6 радиан
Ниже в таблице представлены основные формулы прямолинейного и вращательного движения.
| Прямолинейное движение | Вращательное движение |
|
s - линейное перемещение V - линейная скорость a - линейное ускорение V = Δs/Δt a = ΔV/Δt s = V0(t1 - t0) + sa(t1 - t0)2 V12 - V02 = 2as |
Θ - угловое перемещение ω - угловая скорость α - угловое ускорение ω = ΔΘ/Δt α = Δω/Δt Θ = ω0(t1 - t0) + sα(t1 - t0)2 ω12 - ω02 = 2αΘ |
Еще по теме:
