Применение второго закона Ньютона для вращательного движения
Согласно второму закону Ньютона, ускорение тела под действием силы пропорционально величине силы и обратно пропорционально массе объекта:
a = F/m
Зададимся вопросом, действует ли второй закон Ньютона для вращательного движения?
Используя аналоги характеристик поступательного и вращательного движений второй закон Ньютона для вращательного движения будет иметь вид:
α = M/I
- роль ускорения а выполняет угловое ускорение α;
- роль силы F - момент силы М;
- массу m - заменяет момент инерции I.
Допустим, что тело движется по окружности под действием приложенной по касательной к окружности тангенциальной силой, которая приводит к увеличение тангенциальной скорости мячика, не путать с нормальной силой, направленной вдоль радиуса окружности вращения (подробно тангенциальная и нормальная скорость рассмотрена на странице "Параметры вращательного движения").
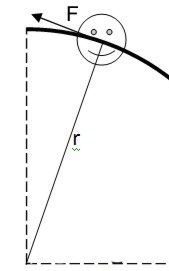
Умножим обе части равенства, описывающего второй закон Ньютона, на радиус окружности r:
a·r = F·r/m
Как известно, F·r=М, поэтому:
a·r = М/m М = a·r·m
Таким образом, мы совершили переход от второго закона Ньютона для поступательного движения к его аналогу для движения вращательного. Следует отметить, что данная формула справедлива только для материальной точки, для протяженного объекта необходимо использовать другие формулы, которые будут рассмотрены позже.
Чтобы завершить переход от описания поступательного движения к вращательному, используем связь между угловым ускорением α и тангенциальным ускорением а:
r·α = a
Совершаем подставку одной формулы в другую и получаем:
М = a·r·m r·α = a M = m·r2·α
Полученная формула связывает момент силы, действующей на материальную точку, и ее углового ускорения. Связь осуществляется через коэффициент пропорциональности m·r2, который называют моментом инерции материальной точки и обозначают I (измеряется в кг·м2).
В итоге, мы получили эквивалент второго закона Ньютона для вращательного движения:
M = I·α
В том случае, если на тело действует одновременно несколько сил, второй закон Ньютона принимает следующий вид:
ΣF = m·a
ΣF - векторная сумма всех сил, которые действуют на объект.
В случае, если на объект действуют одновременно несколько моментов сил, второй закон Ньютона примет вид:
ΣM = I·α
ΣМ - векторная сумма всех моментов сил, которые действуют на объект.
