Как измерить скорость объекта, используя закон сохранения импульса
Как известно, дети полны энергии, которая из них "бьет ключом". Чтобы убедиться в этом, достаточно посетить во время переменки коридор средней школы у дверей кабинета, в котором обучаются школьники начальных классов. Постараемся решить гипотетическую задачу, когда первоклассник Петя, имеющий массу 30 кг, мчится со скоростью 3 м/с и сталкивается с неподвижно стоящим одноклассником Колей, который имеет такую же массу - 30 кг. Спрашивается, с какой скоростью будет после столкновения двигаться тандем Коля+Петя.
Чтобы упростить решение задачи, пренебрегаем всеми внешними силами, включая силу трения, считая, таким образом, что наша система является замкнутой.
Согласно закону сохранения импульса, горизонтальные проекции импульсов (начальный импульс - р0; конечный импульс - р1) учеников равны:
р1 = р0Подставляем в формулу массу и начальную скорость Пети, который обладал определенным импульсом (импульс Коли был равен нулю, поскольку он стоял на месте):
р1 = р0 = mПvП0Поскольку конечный импульс р1 должен быть равен произведению общей массы учеников (mП + mК) на их конечную скорость vПК1, получаем следующую формулу:
р1 = (mП + mК)vПК1Из двух последних уравнений получаем равенство:
р1 = (mП + mК)vПК1 = р0 = mПvП0Отсюда конечная скорость учеников будет равна:
vПК1 = mПvП0/(mП + mК)Подставив значения в формулу получим:
vПК1=(30кг·3м/с)/(30кг+30кг)=1,5м/с.Таким образом, тандем Коля+Петя после их столкновения будет двигаться со скоростью 1,5 м/с, что ровно в 2 раза ниже начальной скорости Пети, что, в общем-то, логично, поскольку масса движущихся объектов после столкновения увеличилась ровно в 2 раза.
Как с помощью закона сохранения импульса измерить начальную скорость пули
Никогда не смотрели передачу "Разрушители легенд" (MythBusters), которая с 2003 года идет на канале Discovery Channel? Посмотрите, не пожалеете. В ходе передачи американские специалисты Джейми Хайнеман и Адам Сэвидж, используя свои навыки и опыт, проводят экспериментальную проверку различных слухов, легенд, мифов и прочих "небылиц", выясняя, могут ли они быть реализованы в реальной жизни людей (например, действительно ли бутерброд всегда падает маслом вниз).
В некоторых сериях Джейми и Адам проводят опыты с огнестрельным оружием, например, в одном эксперименте они выясняли, может ли звуковая волна от движения пули разрушить стеклянный бокал.
Давайте на короткое время представим себя на месте разрушителей легенд и в теории измерим скорость пули, вылетающей из ствола винтовки или пистолета.
Для решения задачи будем использовать специальный маятник, который будет отклоняться на определенный угол после попадания в него пули, и закон сохранения импульса.
В начальный момент времени (положение 1) пуля движется с некой начальной скоростью по направлению к мишени, закрепленной на маятнике, которая находится в покое.
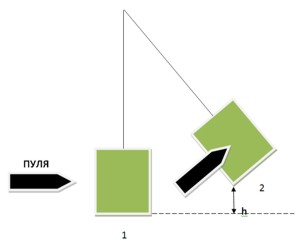
Начальный суммарный импульс пули и мишени равен:
p0=mv0
Конечный суммарный импульс пули, застрявшей в мишени (положение 2):
p1 = (m+M)v1
Для простоты эксперимента мы пренебрегаем потерями энергии на преодоление трения при попадании пули в мишень, поэтому, начальный и конечный импульсы системы пуля+мишень равны:
p0 = p1
Отсюда:
mv0 = (m+M)v1
Искомая величина начальной скорости пули будет равна:
v0 = (m+M)v1/m
Для ее нахождения нам надо знать конечную скорость системы пуля+мишень. В этом нам поможет наш маятник - после попадания пули в мишень, последняя отклонится на определенный угол, поднявшись при этом на высоту h, на которой скорость системы мишень+пуля станет равной нулю. В этой точке кинетическая энергия, которая выражается формулой (m+M)v12/2, преобразуется в потенциальную (m+M)gh. Согласно закону сохранения энергии:
(m+M)v12/2 = (m+M)gh
Отсюда выводим формулу для расчета конечной скорости системы мишень+пуля:
v1 = √2gh
Подставляем эту формулу в прежнее выражение для нахождения начальной скорости пули:
v0 = (m+M)v1/m
Получаем:
v0 = (m+M)(√2gh)/m
Если предположить, что масса пули равна 10 г, а мишень весит 10 кг (104 г), при этом после попадания пули в мишень система мишень+пуля отклонилась на некоторый угол, поднявшись на высоту 10 см, то начальная скорость пули будет равна:
v0=(10+104)·(√2·9,8·0,1)/104=1400м/с
