Маятник - пример простого гармонического движения
Знакомство с простым гармоническим движением проводилось нами на примере колебания груза, прикрепленного к упругой пружине.
Еще одним типичным примером простого гармонического движения является колебания математического маятника (идеализированной системы, которая состоит из невесомой нерастяжимой нити, на которой подвешен груз, масса которого сосредоточена в одной материальной точке).
Попробуем вывести аналогичные математические формулы, описывающие простое гармоническое движение такого маятника.
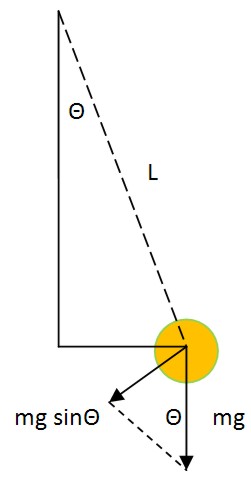
Предположим, что на нити длиной L подвешен груз массой m, при этом маятник отклонен на угол Θ от положения вертикального равновесия.
В таком случае, на груз будет действовать сила гравитационного притяжения F=mg. При этом, движению груза будет препятствовать компонента силы, направленная перпендикулярно нити:
F⊥ = -mg·sin(Θ)
Угловое ускорение маятника α будет определяться через момент компоненты силы F⊥:
M = L·F⊥ = -Lmg·sin(Θ) M = mL2α α = -(g/L)·sin(Θ)
При достаточно малых углах колебания маятника sin(Θ)≈Θ:
α = -(g/L)·Θ
Поскольку в простом гармоническом движении перемещение и ускорение связаны коэффициентом пропорциональности (в нашем случае g/L=ω2), получаем следующее равенство:
ω = √(g/L)
Вспоминаем о цикле (ω=2πf) и периоде (ω=2π/T) колебаний:
f = (1/2π)·√(g/L) T = 2π·√(L/g)
Как видно из полученных формул, период колебаний математического маятника не зависит от массы груза.
