Физика - это просто!

МЕХАНИКА

· Измерения. Системы измерений
· Перемещение
· Скорость
· Ускорение
· Нестандартные связи
· Векторы
· S, V, a - векторные величины
· Первый закон Ньютона
· Второй закон Ньютона
· Третий закон Ньютона
· Гравитация
· Трение
· Свободное падение
· Вращательное движение
· Закон всемирного тяготения
· Работа
· Энергия
· Импульс
· Закон сохранения импульса
· Измерение скорости с помощью ЗСИ
· Параметры вращательного движения
· Вращательное движение и векторы
· Момент силы
· Условие равновесного состояния
· Вращательное движение и 2 закон Ньютона
· Момент инерции протяженного объекта
· Энергия и работа при вращательном движении
· Момент импульса
· Закон Гука
· Простое гармоническое движение
· Энергия гармонического движения
· Маятниковое движение

ТЕРМОДИНАМИКА

ЭЛЕКТРОМАГНЕТИЗМ

ФИЗИКА-ВУЗ

Параметры вращательного движения

Возможно, что колесо, изобретенное человеком давным-давно, явилось главным его изобретением, позволившим решить многие инженерные задачи. Развитие технического прогресса абсолютно невозможно без колеса и многих его производных.

Основные формулы прямолинейного движения и их аналоги в движении вращательном.

Прямолинейное движение	Вращательное движение
v = Δs/Δt v - скорость; Δs - перемещение; Δt - время перемещения.	ω = ΔΘ/Δt ω - угловая скорость; ΔΘ - угол поворота; Δt - время поворота на угол ΔΘ.
a = Δv/Δt a - ускорение; Δs - изменение скорости; Δt - время изменения скорости	α = Δω/Δt α - угловое ускорение; Δω - изменение угловой скорости; Δt - время изменения угловой скорости.
Δs = v0(t1-t0)+1/2a(t1-t0)2 v0 - начальная скорость; t0 - начальный момент времени; t1 - конечный момент времени.	Θ = ω0(t1-t0)+1/2a(t1-t0)2 ω0 - начальная угловая скорость t0 - начальный момент времени; t1 - конечный момент времени.
v12-v02 = 2aΔs v1 - конечная скорость	ω12-ω02 = 2aΔs ω1 - конечная скорость

В повседневной жизни большинство объектов движутся по сложным траекториям, которые, как правило, состоят из поступательного и вращательного движений.

Поступательным движением называют такое движение тела, при котором любая прямая, связанная с движущимся объектом, всегда остается параллельной самой себе.

Вращательным движением называют такое движение, при котором все точки тела движутся по окружностям.

В свою очередь, вращательное движение подразделяется на тангенциальную и радиальную составляющие:

• Тангенциальное движение - часть вращательного движения, происходящего по касательной к окружности вращения, скорость тангенциального движения материальной точки называют линейной скоростью вращательного движения.
• Радиальное (нормальное) движение - часть вращательного движения, происходящего перпендикулярно (по нормали) к касательной или вдоль радиуса окружности.

Параметры прямолинейного и вращательного движений можно связать следующими формулами:

Δs = r·ΔΘ
v = r·ω
a = r·α

На рисунке ниже представлен пример вращательного движения:

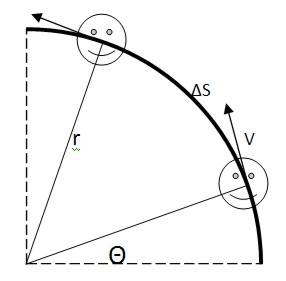
Объект движется по окружности с радиусом r и линейной скоростью v, которая является векторной величиной (обладает величиной и направлением, перпендикулярным радиус-вектору r).

Используя описанные выше формулы, попробуем решить несложную задачу, и определить с какой скоростью движется автомобиль, если его колеса, радиусом 50 см, вращаются с угловой скоростью 10π?

Для решения поставленной задачи воспользуемся формулой связи линейной и угловой скорости:

v = r·ω

Подставим значения, и получим:

v = 0,5·10·π = 15,7 м/с

Тангенциальное ускорение

Тангенциальным ускорением называют скорость изменения величины линейной скорость вращательного движения.

Попробуем связать линейное и угловое ускорения.

Формула линейного ускорения имеет вид:

a = Δv/Δt

• a - линейное ускорение;
• Δv - изменение линейной скорости;
• Δt - время изменения линейной скорости.

Формула углового ускорения имеет вид:

α = Δω/Δt

• α - угловое ускорение;
• Δω - изменение угловой скорости;
• Δt - время изменения угловой скорости.

Между собой линейная и угловая скорости связаны формулой:

v = r·ω

Подставим это выражение в формулу линейного ускорения:

a = Δv/Δt = Δ(r·ω)/Δt

Преобразуем полученное выражение, вынеся за скобки радиус, поскольку он является постоянной величиной:

a = r·Δω/Δt

Учитывая формулу углового ускорения, производим замену:

α = Δω/Δt
a = r·Δω/Δt
a = r·α

В итоге, получена формула связи линейного и углового ускорения:

a = r·α

Тангенциальное ускорение равно произведению радиуса на угловое ускорение.

Центростремительное ускорение

Центростремительным ускорением называют ускорение, которое необходимо для удержания объекта на круговой орбите вращательного движения.

Попробуем связать центростремительное ускорение с угловой скоростью.

Центростремительное ускорение вычисляется по формуле:

aц = v2/r

Линейная и угловая скорости связаны отношением:

v = r·ω

Подставляем одну формулу в другую:

aц = (r·ω)2/r = r·ω2

Таким образом, зная угловую скорость объекта и радиус его движения, можно определить величину центростремительного ускорения объекта.

Применим теоретические знания на практике, и рассчитаем центростремительную силу, необходимую для удержания Земли на своей орбите (принимать во внимание гравитационные воздействия других планет Солнечной системы не будем).

Земля делает полный оборот вокруг Солнца за 365 дней (это не совсем так, но не будем углубляться в нюансы, нам важен сам принцип вычисления). Другими словами, за 365 дней Земля проходит путь в 2π радиан. Таким образом, угловая скорость движения Земли равна:

ω = ΔΘ/Δt = 2·π/365

Преобразуем дни в секунды, чтобы получить значение угловой скорости в стандартных единицах: 365 дней = 31 536 000 секунд = 3,1536·10⁷.

Подставляем значение в секундах в предыдущую формулу:

ω = 2·π/(3,1536·107) = 2·10-7 с-1

Средний радиус земной орбиты равен 150 млн. км или 1,5·10¹¹ м. Подставляя числовые значения в формулу центростремительного ускорения получим:

aц = r·ω2
aц = (1,5·1011)·(2·10-7)2 = 6·10-3 с-1

Масса Земли примерно равна 6·10²⁴ кг. Вычисляем центростремительную силу, необходимую для удержания Земли на ее орбите:

Fц = m·aц
Fц = (6·1024)·(6·10-3) = 3,6·1022 Н.