Решение уравнений вида tg(x)=y, ctg(x)=y
Принципиальное отличие решения уравнений tg(x)=y, ctg(x)=y от решения уравнений вида sin(x)=y, cos(x)=y, заключается в том, что у тангенса и котангенса y может принимать любые значения, тогда, как у косинуса только в диапазоне от -1 до 1 включительно.
В уравнении вида tg(x)=y, x не может принимать значения (π/2+π·n), где n - целое число, поэтому, график тангенсоиды состоит из набора отдельных кривых:
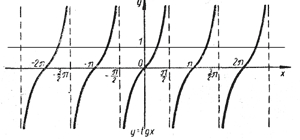
Решением уравнения tg(x)=1 на промежутке от (-π/2; π/2) будет:
x = arctg(1) = (π/4)
Решением уравнения tg(x)=y будет бесконечное множество углов, которые можно определить по формуле:
x = arctg(y)+π·n
Полным решением уравнения tg(x)=1 будет множество углов, вычисляемых по формуле:
x = (π/4)+π·n
Для уравнений вида ctg(x)=y:
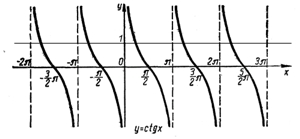
x = arcctg(y)+π·n
Решением уравнения ctg(x)=1 будет бесконечное множество углов, которые можно определить по формуле:
x = arcctg(1)+π·n x = (π/4)+π·n
