Решение неравенств с одним неизвестным
Линейные неравенства с одним неизвестным имеют вид:
Ax>B Ax<B Ax≥B Ax≤B
- A и B - заданные числа;
- x - неизвестное.
Число будет являться решением неравенства с одним неизвестным в том случае, если после его подстановки в неравенство вместо неизвестного х числовое неравенство будет верным.
Например, одним из решений неравенства 5+x>4 будет x=1, т.к., 5+1>4 - это верное неравенство.
Чтобы решить неравенство, следует найти все множество чисел, делающих неравенство верным или доказать, что никакое число не будет делать равенство верным, т.е., неравенство не будет иметь решений.
Для решения неравенств пользуются свойствами неравенств:
- при переносе слагаемого в другую часть неравенства, у переносимого слагаемого знак меняется на противоположный, при этом знак самого неравенства не изменяется;
- обе части неравенства можно умножать или делить на одно и то же число, отличное от нуля, при этом, в случае умножения/деления на положительное число знак неравенства не изменяется; в противном случае, знак неравенства меняется на противоположный.
Решение неравенств очень удобно представлять в графическом виде на числовой прямой.
Пример 1:
4+x≥9 x≥9-4 x≥5

На числовой прямой решением данного неравенства будет луч, начинающийся в точке 5 и идущий вправо, черный кружок, которым обозначено начало луча, говорит о том, что число 5 включается в число решений рассматриваемого неравенства.
Пример 2:
4+x<1 x<1-4 x<(-3)
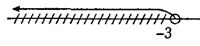
На числовой прямой решением данного неравенства будет луч, начинающийся в точке -3 и идущий влево, белый кружок, которым обозначено начало луча, говорит о том, что число -3 не включается в число решений рассматриваемого неравенства.
