Математика - это просто!

УРАВНЕНИЯ и ТОЖДЕСТВА

· Алгебраические равенства
· Работа со скобками
· Уравнение с одним неизвестным
· Тождества
· Линейное уравнение
· Система из 2 уравнений
· Квадратное уравнение
· Теорема Виета
· Биквадратное уравнение
· Примеры решения задач
· Уравнение вида sin(x)=y
· Уравнение вида cos(x)=y
· Уравнение вида tg(x)=y; ctg(x)=y
· Показательные уравнения
· Логарифмические уравнения
НЕРАВЕНСТВА
· Числовые неравенства
· Сложение и умножение
· Решение неравенств
· Числовые промежутки
· Модуль числа
· Квадратные неравенства
· Тригонометрические неравенства
· Показательные неравенства
· Логарифмические неравенства

НАТУРАЛЬНЫЕ ЧИСЛА

ДРОБИ

ОДНОЧЛЕНЫ и МНОГОЧЛЕНЫ

ФУНКЦИИ

ТРИГОНОМЕТРИЯ

ПЛОСКИЕ ФИГУРЫ

ВЫСШАЯ МАТЕМАТИКА

Как решать квадратные неравенства

Неравенство в одной части которого стоит квадратный трехчлен вида ax²+bx+c, а в другой "ноль", называется квадратным неравенством.

В решении квадратных неравенств широко используют график квадратичной функции, представляющий из себя параболу.

Алгоритм решения квадратного неравенства при помощи графика:

1. найти вершину параболы;
2. определить направление ветвей параболы;
3. найти точки пересечения параболы оси абсцисс, если таковые имеются;
4. построить эскиз параболы, при помощи которого определить промежутки, на которых выполняется неравенство.

С помощью графика решим следующее неравенство: 2x²+4x-8≤0.

1. Находим координаты вершины параболы:

x0 = -b/(2a)
x0 = -4/(2·2) = -1

y0 = -(b2-4ac)/4a
y0 = -(42-4·2·(-8))/4·2 = -10

2. Поскольку коэффициент a положителен - ветви параболы направлены вверх.

3. Находим точки пересечения параболой оси абсцисс, для этого решаем квадратное уравнение:

2x2+4x-8 = 0
x1,2 = (-4±√(16+64))/4
x1,2 = -1±√5
x1 ≈ -3,24
x2 ≈ 1,24

4. Строим эскиз параболы (зеленый график):

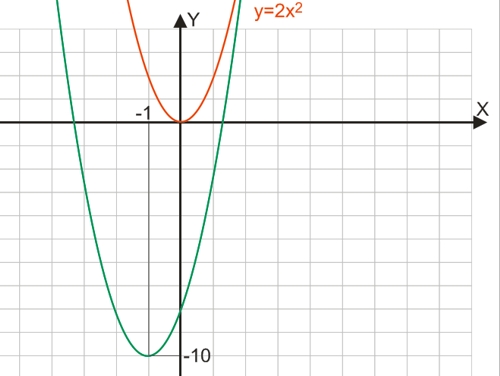
Таким образом, исходному неравенству 2x²+4x-8≤0 будут удовлетворять те значения x, при которых значения функции отрицательны или равны нулю, - на графике это будут те точки параболы, которые располагаются ниже оси абсцисс или лежат на ней:

-1-√5 ≤ x ≤ -1+√5

Второй пример: решить неравенство 2x²<0.

1. Координаты вершины параболы (0;0);
2. Ветви параболы направлены вверх;
3. Парабола касается оси абсцисс в точке с координатами (0;0);
4. Эскиз параболы - красный график на рисунке вверху.

Ответ: Поскольку вся парабола лежит выше оси абсцисс, касаясь ее в точке начала координат, точек, удовлетворяющих исходному неравенству (лежащих ниже оси абсцисс), нет - неравенство не имеет решения.