Что такое описанная окружность
Любой многоугольник, все вершины которого принадлежат одной и той же окружности, называется вписанным в эту окружность, а сама окружность - описанной около такого многоугольника.

На рисунке вверху изображен четырехугольник ABCD, вписанный в окружность (красный цвет) с центром в точке О. Все вершины четырехугольника лежат на окружности. Такая окружность назвается описанной около четырехугольника ABCD.
Свойства четырехугольника, вписанного в окружность:
- Суммы противоположных углов вписанного четырехугольника равны: ∠A+∠C=∠D+∠B.
- Перпендикуляры, проведенные через середины сторон вписанного четырехугольника (и вообще, любого описанного многоугольника), пересекаются в точке О, являющейся центром описанной окружности;
- Окружность можно описать лишь только вокруг того четырехугольника, суммы противоположных углов которого равны.
На рисунке ниже изображен треугольник ABC, вписанный в окружность (красный цвет) с центром в точке О, - все вершины такого треугольника лежат на описанной окружности.
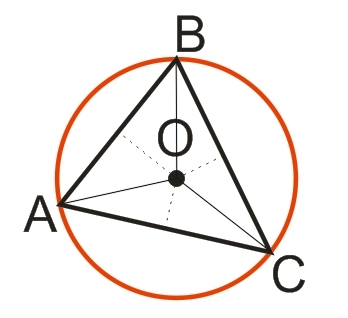
Свойства треугольника, вписанного в окружность:
- Вокруг любого треугольника можно описать окружность и только одну.
- Перпендикуляры, проведенные через середины сторон вписанного треугольника, пересекаются в точке О, являющейся центром описанной окружности;
- Расстояние от точки пересечения серединных перпендикуляров вписанного треугольника до любой из вершин такого треугольника будет равно радиусу описанной вокруг треугольника окружности (радиусы OА, OВ, OС).
