Теорема Пифагора
Теорема Пифагора является одной из самой лаконичных геометрических теорем. Звучит она следующим образом:
Квадрат гипотенузы равен сумме квадратов катетов.
Поскольку в теореме говорится о гипотенузе и катетах, то речь идёт о прямоугольном треугольнике. Отсюда, теорема, обратная теореме Пифагора будет такой:
Если в треугольнике квадрат самой большой стороны равен сумме квадратов двух других его сторон, то такой прямоугольник будет прямоугольным.
Напомним, что прямоугольным называется треугольник, один из углов которого равен 90°.
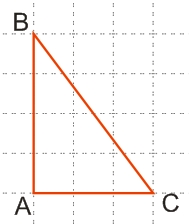
BC2=AC2+AB2
Поскольку, катеты прямоугольного треугольника являются одновременно и его высотами, то площадь прямоугольного треугольника будет равна половине произведения его катетов:
SABC=½·AB·AC
Используя теорему Пифагора, можно легко найти формулу для нахождения площади равностороннего треугольника по его стороне:
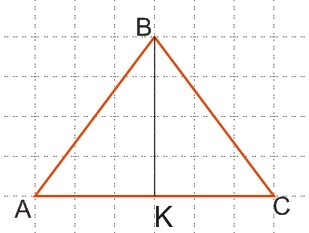
Поскольку нам известна одна сторона треугольника (а у равностороннего треугольника все стороны равны), то, для нахождения его площади нам осталось найти высоту ВК треугольника АВС (см. рисунок выше).
В равностороннем треугольнике высота, медиана и биссектриса совпадают. Поскольку, высота ВК образует перпендикуляр к стороне АС, а медиана ВК делит эту же сторону на две равные части, то у нас получаются два одинаковых прямоугольных треугольника: АВК и СВК.
По теореме Пифагора:
AB2=AK2 + BK2 BK2=AB2 - AK2 BK2=AB2 - (AB/2)2 BK2=AB2 - (AB2/4) BK2=4AB2/4 - AB2/4 BK2=(4AB2 - AB2)/4 BK2=3AB2/4 BK=(AB/2)·√3 S=½·AB·BK S=½·AB·(AB/2)·√3 S=AB2(√3)/4
Средняя линия треугольника
Средней линией треугольника называется отрезок, соединяющий середины двух любых его сторон:
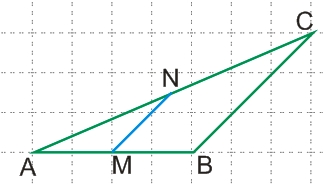
Стороны треугольника, соединенные средней линией, называются боковыми сторонами (стороны АС и АВ на рисунке), а третья сторона (ВС) - основанием.
Свойства средней линии треугольника:
- средняя линия параллельна основанию треугольника (MN || BC);
- длина средней линии треугольника равна половине длины его основания (MN = ½BC).
