Теорема синусов треугольника
Отношения длин сторон треугольника к их противолежащим углам - равны.
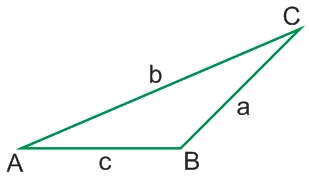
a/sin(A) = b/sin(B) = c/sin(C)
Теорема синусов позволяет находить все углы и длины сторон треугольника, если известны:
- два любых угла треугольника и одна из его сторон;
- две любые стороны треугольника и один из двух противолежащих им углов.
Пример 1. Построить треугольник АВС, у которого известны одна сторона и два угла: АВ=10 см, ∠B=30°, ∠C=60°.
Решение. По теореме синусов:
b/sin(B) = c/sin(C) АС/sin(B) = АВ/sin(C)
Отсюда находим сторону АС:
АС = АВ·sin(B)/sin(C) AC = 10·sin(30°)/sin(60°) AC = 10·(1/2)/(√(3)/2) AC = 10/√3 ≈ 5,77 см.
Для нахождения третьей стороны BC сначала найдем угол А: 180°-30°-60°=90°.
Теперь снова используем теорему синусов:
b/sin(B) = а/sin(А) АС/sin(B) = BC/sin(A) BC = AC·sin(A)/sin(B) BC = (10/√3)·sin(90°)/sin(30°) BC = (10/√3)·1/(1/2) BC = 20/√3 ≈ 11,55 см
Ответ: AC = 10/√3; BC = 20/√3; ∠A=90°
Пример 2. Построить треугольник АВС, если известны две стороны и угол, противолежащий одной из них: ВС = 3 см, AC = 4 см, ∠A = 30°.
Решение. Согласно теореме синусов:
BC/sin(A)=AC/sin(B) sin(B)=AC·sin(A)/BC sin(B)=4·sin(30°)/3 sin(B)=4·(1/2)/3 sin(B)=2/3 ≈ 0,67
Казалось бы, что задача решена, однако, не надо забывать, что такие тригонометрические функции, как синус и косинус, являются очень "коварными" - нюанс заключается в том, что значение sin(B)=2/3 ≈ 0,67 могут принимать два угла в 42° и 138° (см. Что такое синус).
Фактически с такими данными могут быть построены два треугольника.
По этой причине, используя теорему синусов, следует найти оба варианта:
Если ∠B=42°:
∠C = 180°-42°-30° = 108° AB=BC·sin(C)/sin(A) AB ≈ 5,7 см
Если ∠B=138°:
∠C = 180°-138°-30° = 12° AB=BC·sin(C)/sin(A) AB ≈ 1,26 см
Ответ: возможно построить два треугольника АВС:
- ∠B=42° ∠C=108° AB ≈ 5,7 см
- ∠B=138° ∠C=12° AB ≈ 1,26 см
