Что такое вектор
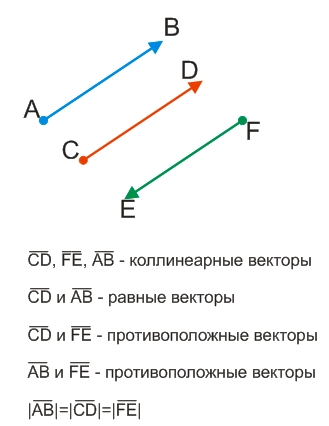
Направленный отрезок называется вектором.
Отрезок называется направленным, если у него указаны начало и конец, т.е., указано направление.
Начало вектора обычно обозначают точкой, а конец - стрелкой.
Вектор, как и отрезок, обозначается двумя буквами, одна из которых обозначает один конец отрезка, а вторая - другой его конец, но с той разницей, что точка, обозначающая начало вектора, обязательно указывается первой, в то время, как у отрезка не имеет значение какой из его концов будет указан первым.
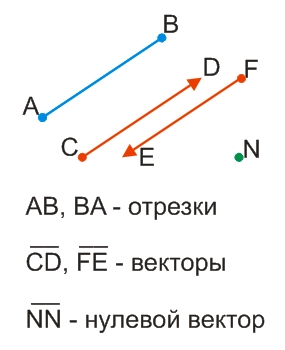
О том, что данный отрезок является вектором, говорит горизонтальная черта над буквами, обозначающими вектор.
Условия равенства векторов:
- векторы лежат на одной и той же прямой, либо на параллельных прямых;
- направления векторов совпадают;
- длины векторов равны.
Любая точка плоскости является вектором начало и конец которого совпадают - это, так называемый, нулевой вектор.
Длиной вектора или модулем вектора называется длина отрезка, обозначающего этот вектор.
|CD| = 5 см |NN| = 0
Коллинеарными называются вектора, лежащие на одной и той же прямой или принадлежащие параллельным прямым.
Нулевой вектор считается коллинеарным любому вектору.
Два ненулевых коллинеарных вектора считаются сонаправленными, если их направления совпадают.
Нулевой вектор считается сонаправленным любому вектору.
Два ненулевых коллинеарных вектора считаются противоположно направленными, если их направления противоположны.
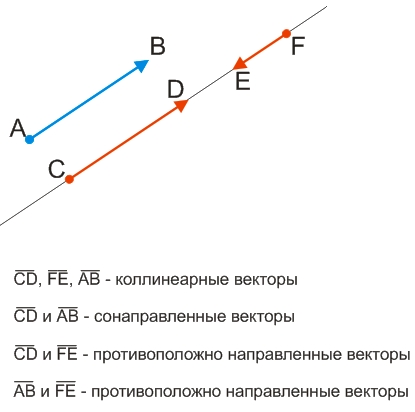
Два сонаправленных вектора считаются равными, если они имеют одинаковую длину (модуль).
Два противоположно направленных вектора, имеющих одинаковые модули, называются противоположными (следует различать противоположно направленные векторы и противоположные векторы).