Касательная к окружности
Прямая, имеющая только одну общую точку с окружностью (точку касания), называется касательной к этой окружности.
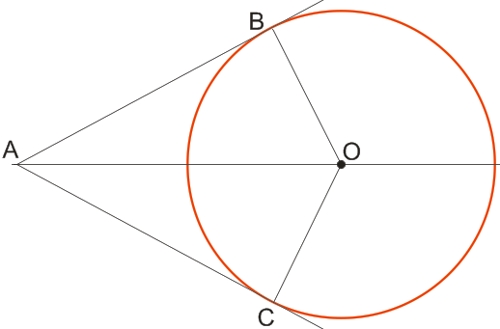
Если точка B является точкой касания прямой AB к окружности с центром О, то AB⊥OB.
Если AB⊥OB и точка B принадлежит к окружности с центром в точке О, то прямая АВ является касательной к этой окружности.
Если к окружности с центром О провести две касательные АВ и АС из одной и той же точки А, то луч АО будет являться биссектриской угла BAC.
Для доказательства надо провести из центра О к точкам касания радиусы OB и OC.Поскольку радиусы OB и OC являются перпендикулярами к прямым АВ и АС, то получим два прямоугольных треугольника АОВ и АОС с общей гипотенузой АО.
Прямоугольные треугольники АОВ и АОС будут равны, поскольку гипотенуза у них общая, а катеты ОВ и ОС являются радиусами одной и той же окружности.
Из равенства треугольников вытекает равенство сторон АВ и АС, а также равенство углов BAO и CAO, сумма которых составляет угол BAC, поэтому, общая гипотенуза будет являться в то же время и биссектрисой угла BAC.
