Что такое окружность
Окружностью называют совокупность точек плоскости, равноудаленных от некой одной точки, которая называется центром окружности.
Расстояние, на котором расположены точки окружности от ее центра, называется радиусом окружности. Это расстояние, как правило, обозначается литерой R или r.
Отрезок, соединяющий любые две точки окружности, называется хордой окружности.
Хорда, проходящая через центр окружности, называется диаметром окружности (обозначается D или d). Длина диаметра окружности равна длине двух её радиусов: D=2R.
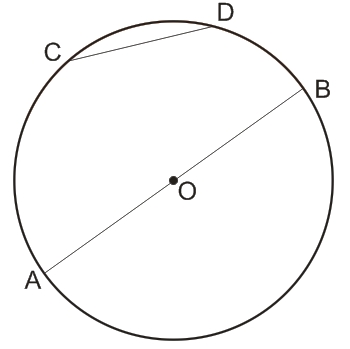
- CD - хорда;
- АВ - диаметр;
- АО и ОВ - радиусы.
Длина окружности обозначается литерой С.
С = 2πR = πD
Число π является "связующим звеном" между длиной окружности и её радиусом (диаметром). Число π является константой - бесконечной десятичной дробью: π = 3,1415926....
Центральный угол окружности
Угол, вершина которого совпадает с центром окружности, называется центральным углом окружности.
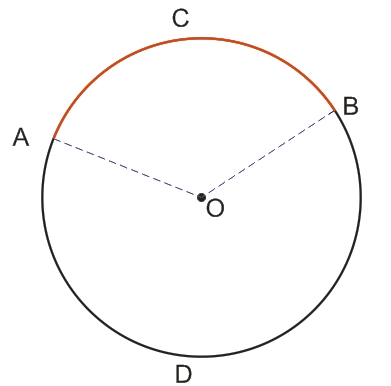
Дуга окружности, заключенная между сторонами центрального угла, называется дугой, на которую опирается центральный угол.
Центральный угол может опираться на две дуги, одна из которых больше длины полуокружности, а вторая меньше. Частным случаем центрального угла является развернутый угол (180°), который опирается на две полуокружнсоти:
- центральный угол АОВ опирается на дугу АСВ (красный цвет), которая меньше длины полуокружности - в таком случае градусная мера такой дуги считается равной градусной мере самого центрального угла;
- центральный угол AOB опирается на дугу АDВ, которая больше длины полуокружности - в таком случае градусная мера такой дуги считается равной разности 360°-α, где α - величина центрального угла;
Вписанный угол окружности
Угол, вершина которого лежит на окружности, а обе стороны пересекают саму окружность, называется вписанным углом.
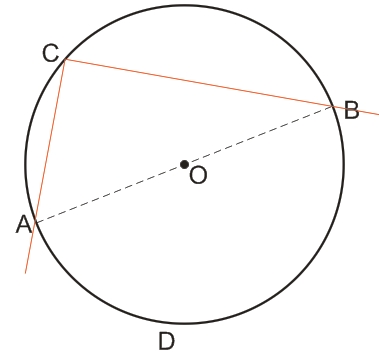
Дуга окружности, лежащая между сторонами вписанного угла, называется дугой, на которую опирается вписанный угол.
Величина вписанного угла равна половине градусной величины дуги, на которую он опирается.
На рисунке выше вписанный угол АСВ опирается на дугу ADB, которая является полуокружностью.
На рисунке ниже вписанный угол ADB (синий цвет) опирается на дугу АСВ, длина которой меньше полуокружности, а вписанный угол АСВ (красный цвет) опирается на дугу ADB, длина которой больше длины полуокружности.
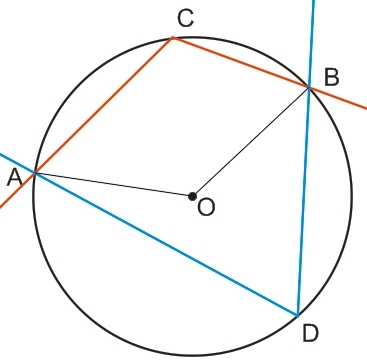
Величина центрального угла АОВ равна 125°. Величина дуги АСВ, на которую опирается этот центральный угол, также равна 125°. Величина другой дуги ADB, на которую опирается этот же угол, равна 360°-125°=235°.
Поскольку вписанный угол вдвое меньше дуги, на которую он опирается, то величина вписанного угла ADB, опирающегося на дугу ACB: 125°/2=62,5°. Соответственно, величина вписанного угла ADB: 235°/2=117,5°.
В образовавшемся вписанном четырехугольнике ACBD сумма противоположных углов равна 180°. Доказать это очень просто, основываясь на изложенной выше информации.
Столь же просто доказать и то, что все вписанные углы, опирающиеся на полуокружность, являются прямыми. Для этого в вышеприведенных расчетах надо лишь подставить другие цифры: 180°/2=90°.
Все вписанные углы, которые опираются на одну и ту же дугу, равны между собой.
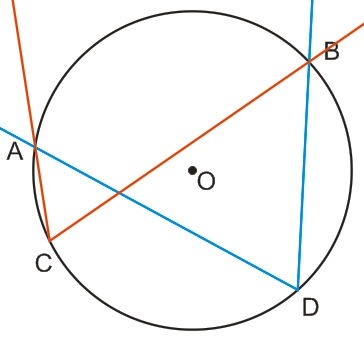
∠ACB=∠ADB, т.к., они опираются на одну и ту же дугу.
