Что такое вписанная окружность
Окружность, касающаяся всех четырех сторон четырехугольника, называется вписанной в этот четырехугольник, а сам четырехугольник - описанным около такой окружности.
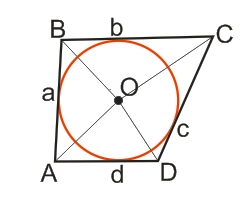
На рисунке вверху изображена вписанная в четырехугольник ABCD окружность (красный цвет), с центром в точке О, которая касается сторон четырехугольника в точках a, b, c, d.
Свойства четырехугольника, описанного около окружности:
- Суммы противоположных сторон описанного четырехугольника равны: AB+CD=AD+CB.
- Биссектрисы всех углов описанного четырехугольника (и вообще, любого описанного многоугольника) пересекаются в точке О, являющейся центром вписанной окружности;
- Окружность можно вписать лишь только в тот четырехугольник, суммы противоположных сторон которого равны.
На рисунке ниже изображена вписанная в треугольник ABC окружность (красный цвет), с центром в точке О, которая касается сторон треугольника в точках a, b, c.
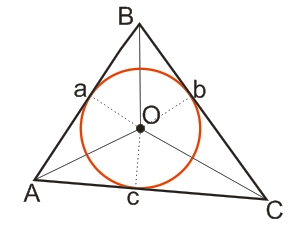
Свойства треугольника, описанного около окружности:
- В любой треугольник можно вписать окружность и только одну.
- Биссектрисы всех углов описанного треугольника пересекаются в точке О, являющейся центром вписанной окружности (биссектрисы АО, ВО, СО пересекаются в точке О);
- Расстояние от точки пересечения биссектрис описанного треугольника до любой из сторон такого треугольника будет равно радиусу вписанной в этот треугольник окружности (радиусы Oa, Ob, Oc).
