Медиана треугольника
Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противолежащей ему стороны.
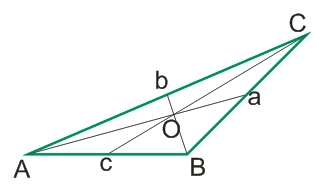
Ab=bC; Ca=aB; Bc=cA.
Медианы всегда пересекаются в одной точке, которая делит каждую медиану в соотношении 2:1:
- AO:Oa = 2:1
- BO:Ob = 2:1
- CO:Oc = 2:1
Биссектриса треугольника
Биссектрисой угла называется луч, проходящий через его вершину и делящий его на два равных угла.
Биссектрисой треугольника называют отрезок биссектрисы угла от его вершины до противолежащей стороны.
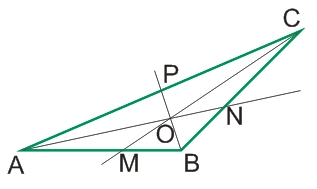
Луч ВР - биссектриса угла В; отрезок ВР - биссектриса угла В треугольника АВС.
Биссектрисы треугольника всегда пересекаются в одной точке.
Биссектриса треугольника делит противолежащую сторону в таком же отношении, в каком находятся стороны треугольника, прилежащие к углу:
- AM/MB = CA/CB
- AP/PC = BA/BC
- BN/NC = AB/AC
Высота треугольника
Высотой треугольника называется перпендикуляр, опущенный из угла треугольника на его противолежащую сторону.
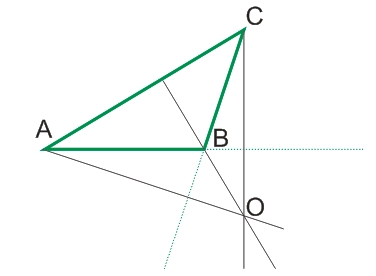
В тупоугольных треугольниках для проведения высот к сторонам, прилежащим к тупому углу, необходимо эти стороны продолжить за пределы треугольника.
Прямые, на которых лежат высоты, в любом треугольнике пересекаются в одной точке, которая может находиться за пределами треугольника.
В прямоугольных треугольниках высоты сходятся в вершине прямого угла.
