Что такое параллелограмм
Прямолинейная плоская фигура, имеющая четыре угла, называется четырехугольником.

Четырехугольник, у которого противоположные стороны параллельны друг другу, назыается параллелограммом.
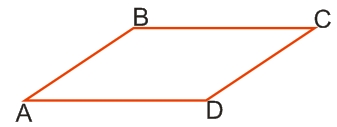
Четырехугольник ABCD, изображенный на рисунке выше, является параллелограммом, т.к., AB || CD и AD || BC.
Линии, соединяющие противоположные углы параллелограмма, называются диагоналями (AC и BD - диагонали параллелограмма ABCD).
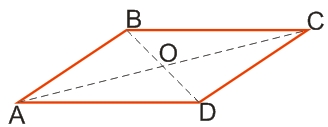
Свойства параллелограмма:
- противоположные стороны параллелограмма равны:
- AB = CD;
- AD = BC.
- противоположные углы параллелограмма равны:
- ∠A = ∠C;
- ∠D = ∠B.
- диагонали параллелограмма в точке их пересечения делятся пополам:
- AO = OC;
- BO = OD.
Признаки параллелограмма
Четырехугольник будет параллелограммом, если:
- Признак 1:
- плоская фигура является четырехугольником;
- длины одной пары противоположных сторон четырехугольника равны;
- длины второй пары противоположных сторон четырехугольника равны.
- Признак 2:
- плоская фигура является четырехугольником;
- длины одной из пар противоположных сторон четырехугольника равны;
- эти же стороны параллельны между собой.
- Признак 3:
- плоская фигура является четырехугольником;
- диагонали четырехугольника в точке их пересечения делятся пополам.
Площадь параллелограмма
Перпендикуляр, опущенный из угла параллелограмма к его противоположной стороне, называется высотой параллелограмма.
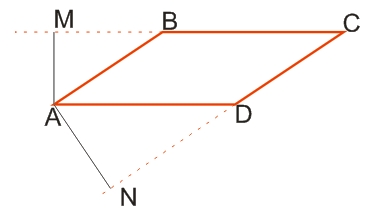
AM, AN - высоты параллелограмма ABCD (AM⊥CM (CB); AN⊥CN (CD)).
Площадь параллелограмма равна произведению одной из его сторон на высоту параллелограмма, проведенную к этой стороне:
SABCD=BC·AM SABCD=CD·AN
