Виды треугольников
Треугольник является простейшей плоской фигурой, которая образована из трех отрезков, соединененных между собой таким образом, что конец одного отрезка является началом другого, при этом отрезки соединяются между собой под углом не равным нулевому или развернутому.
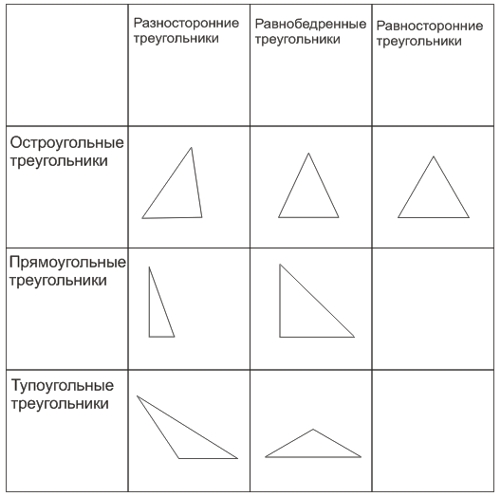
Все треугольники подразделяются по величинам углов и длинам сторон:
- в зависимости от величин углов:
- остроугольные - все углы в треугольнике менее 90°;
- прямоугольные - один из углов треугольника равен 90°;
- тупоугольные - один из углов треугольника больше 90°.
- в зависимости от длин сторон:
- разносторонние - все стороны треугольника разной длины;
- равнобедренные - две из сторон треугольника равны между собой;
- равносторонние - все три стороны треугольника равны между собой.
Соотношения между углами и сторонами треугольника
Углы и стороны в треугольнике тесно взаимосвязаны:
- длина любой из сторон треугольника меньше суммы длин двух других его сторон;
- против большей стороны лежит больший угол;
- против большего угла лежит большая сторона.
Сумма всех углов треугольника всегда равна 180°.
Для того, чтобы найти длины всех сторон треугольника и величины его углов, надо знать:
- два любых угла + длину любой стороны;
- длину двух любых сторон треугольника + величину угла, заключенного между ними;
- длину двух любых сторон треугольника + величину одного из двух противолежащих им углов;
- длину всех сторон треугольника.
