Какие треугольники называются подобными
Треугольники называются подобными, если их углы соответственно равны, а сходственные стороны - пропорциональны.
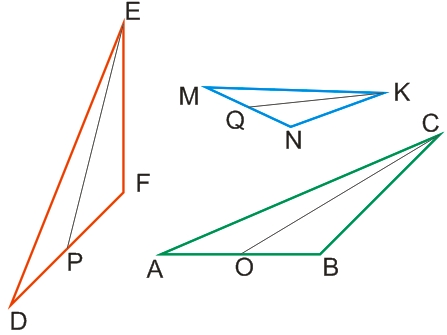
В треугольниках, у которых равны углы, соответственными называются стороны, противолежащие соответственным углам.
На рисунке треугольники ABC, DFE, MNK подобные, т. к.:
- ∠A=∠D=∠M - соответственные углы;
- ∠B=∠F=∠N - соответственные углы;
- ∠C=∠E=∠K - соответственные углы;
- сходственные стороны AB, DF, MN - пропорциональны;
- сходственные стороны BC, FE, NK - пропорциональны;
- сходственные стороны CA, ED, KM - пропорциональны.
Говоря "житейским языком", подобные треугольники получаются путем изменения масштаба и/или вращения вокруг оси.
Коэффициент подобия - отношение сходственных сторон подобных треугольников.
Коэффициент подобия треугольников АВС и DFE равен 1, поскольку AB/DF=BC/FE=CA/ED=1.
Коэффициент подобия треугольников ABС и MNK: AB/MN=BC/NK=CA/KM=3/2.
Медианы, биссектрисы и высоты, проведенные к сходственным сторонам у подобных треугольников, называются сходственными.
У подобных треугольников отношение сходственных медиан, как и отношение сходственных высот, как и отношение сходственных биссектрис равно коэффициенту подобия.
AB/DF=BC/FE=CA/ED=CO/EP=1.
AB/MN=BC/NK=CA/KM=CO/KQ=3/2.
Площади подобных треугольников равны квадрату коэффициента подобия.
Треугольники будут подобными, если:
- они имеют две пары равных углов (если ∠A=∠D; ∠B=∠F, то треугольники ABC и DFE подобные - см. рисунок выше);
- они имеют одну пару равных углов, к которым прилежат пропорционально равные стороны (если ∠A=∠D; AB/DF=AC/DE, то треугольники ABC и DFE подобные - см. рисунок выше);
- все стороны одного треугольника пропорциональны сторонам другого (AB/DF=BC/FE=CA/ED, то треугольники ABC и DFE подобные - см. рисунок выше).
