Углы, образованные пересечением двух прямых секущей
Если какие-либо две прямые, расположенные в одной плоскости, пересекаются третьей прямой (секущей), то образуются 8 углов, некоторые из которых являются парными и носят определенные названия.
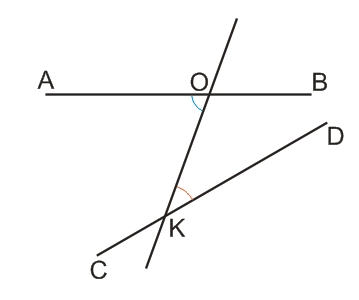
Четыре угла, лежащие между прямыми AB и CD, называются внутренними углами - это углы AOK, BOK,CKO, DKO.
Пары внутренних углов, лежащие по разные стороны от секущей, называются накрест лежащими внутренними углами - это углы AOK - DKO и BOK - CKO.
Пары внутренних углов, лежащие по одну сторону от секущей, называются односторонними внутренними углами - это углы AOK - СKO и BOK - DKO.
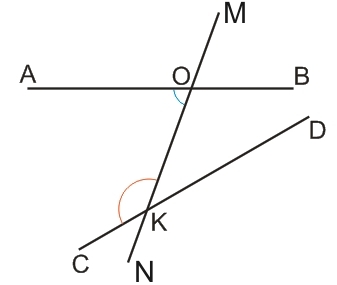
Пары углов, лежащие по одну сторону от секущей, из которых только один является внутренним, - называются соответственными углами - это углы MOB-OKD; BOK-DKN; AOK-CKN; MOA-CKO.
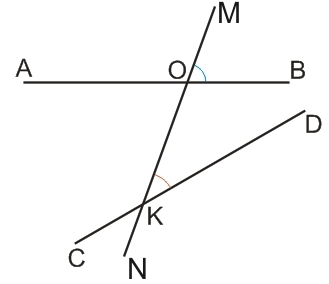
Углы, образованные секущей при пересечении параллельных прямых
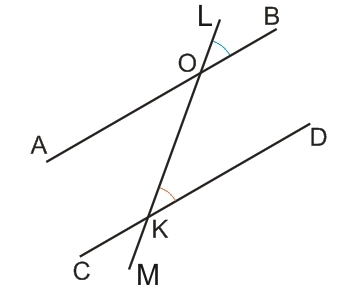
Если секущая (LM) пересекает две параллельные прямые (AB, CD), то:
- накрест лежащие углы равны между собой (угол АОМ равен углу LKD);
- соответственные углы равны между собой (угол LOB равен углу LKD);
- сумма односторонних углов равна 180° (∠BOM+∠LKD=180°).
